2

Let $S$ denotes the area, $L$ the perimeter, and $R=\sqrt{S}/L$. I am computing some distributions related to these triangles, assuming they are randomly distributed. By random, I mean the three vertices are uniformly distributed on a circle of radius $\rho$. The reason that I am interested in $R$ is because this ration does not depend on the radius $\rho$ of the circle in question. It is invariant to the distribution of $\rho$, and independent of the unit used for measurements.

Of course the equilateral triangle has maximum area, but it also has maximum perimeter. Thus even though the maximum value of $R$ is very close to that corresponding to an equilateral triangle, it might not necessarily be exactly identical.

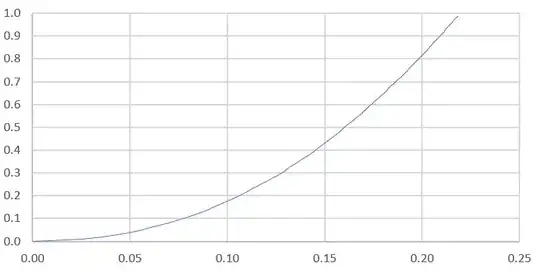
The plot below shows the distribution for $R$, that is $P(R<r)$ with $r$ on the X-axis and $P(R<r)$ on the Y-axis. Here $R$ is viewed as a random variable, as the vertices are random.

My question: My can you compute the maximum for $R$, exactly? Assume, without loss of generality, that the vertices are on the unit circle centered at the origin ($\rho=1$), and that one vertex is $(1,0)$. This eliminates several degrees of freedom. The max value for $R$ is around $0.25$.

enter image description here

Vincent Granville
  • 3,605
  • This is interesting information, but what question are you hoping for others to answer? – Vaekor Nov 02 '21 at 20:27
  • @Vaekor: My question: can you compute the maximum for $R$? Assume, without loss of generality, that the vertices are on the unit circle centered at the origin ($\rho=1$), and that one vertex is $(1,0)$. This eliminates several degrees of freedom. The max value for $R$ is around $0.25$. – Vincent Granville Nov 02 '21 at 20:31
  • I suspect the answer corresponds to the equilateral triangle, yielding $R=\frac{3^{1/4}}{6}$. – Vincent Granville Nov 02 '21 at 20:48
  • Connected : https://math.stackexchange.com/q/414668 – Jean Marie Nov 02 '21 at 21:17

2 Answers2

4

For a moment, consider that any triangle could be considered a triangle inscribed in a circle, as any triangle could retroactively have a circle circumscribed around it. Therefore, just as we could consider a specific radius to make our case, we could also set perimeter constant.

In this case, however, it has already been shown (in Given a polygon of n-sides, why does the regular one (i.e. all sides equal) enclose the greatest area given a constant perimeter? and others) that the equilateral triangle will enclose the greatest area for the perimeter.

Therefore, in your case, $R=\frac{\sqrt[4]{3}}{6}$ has to be your optimum value, because for any other triangle, your area will be suboptimal for that perimeter, giving a lesser value.

Vaekor
  • 524
  • 2
  • 7
1

You may use the formulae for circumscribed circle:

$$2\rho=\frac{abc}{2S},\text{ and } a+b+c\le 3\sqrt{3}\rho$$

Assuming unit circle: $$2=\frac{abc}{2S}$$ and $$a+b+c\le3\sqrt{3}$$ with equality when $a=b=c$ (see also Maximum perimeter for triangle inscribed in circle)

Then simply use AM-GM:

$$R=\frac{\sqrt{S}}{a+b+c}=\frac{1}{2(a+b+c)}\sqrt{abc}\le\frac{1}{2(a+b+c)}\left(\frac{a+b+c}{3}\right)^{3/2}=\frac{1}{6\sqrt{3}}\sqrt{a+b+c}\le\frac{1}{6\sqrt{3}}\sqrt{3\sqrt{3}}=\frac{3^{1/4}}{6}$$ which was to be proved.

Momo
  • 16,027