I can't get the formula right.
There is a formula for an equilateral polygon
I'm trying to translate it into code to draw a five-pointed star
Here's how I translated the equation:
_mytKrg.integerVector.append(_mytKrg.X + (_mytKrg.R * cos(2*sin(1)+M_PI*3)/(2*5))/((cos(2*sin(cos(1*5*grad_kol_toch)))+M_PI*3)/(2*5))); //point Х
_mytKrg.integerVector.append(_mytKrg.Y + (_mytKrg.R * sin(2*cos(1)+M_PI*3)/(2*5))/((sin(2*cos(sin(1*5*grad_kol_toch)))+M_PI*3)/(2*5))); //point У
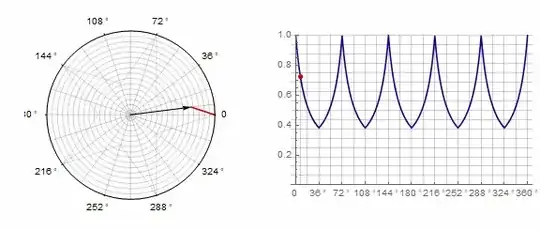
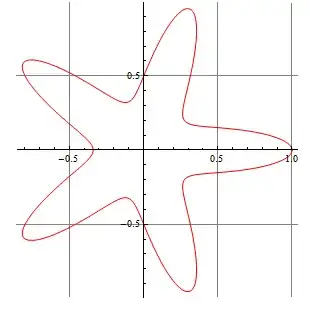
here is the result :
Here's the whole code:
zvezda.pro
#ifndef KRUG_QT_H
#define KRUG_QT_H
#include <QMainWindow>
#include <QDebug>
#include <QPainter>
#include <QPen>
#include <QFont>
#include <QtMath>
#include <QPointF>
// структура для отрисовки круга
struct strKryg
{
strKryg()
{
R = 0.0; kol_toch = 0;
tocka_1 = 0; tocka_2 = 0;
X = 0.0; Y = 0.0;
integerVector.clear();
point_for_line.clear();
}
float R; // радиус
int kol_toch; // колич точек которые будут формировать круг
int tocka_1; // точка выреза начало
int tocka_2; // точка выреза конец
float X; float Y; // расположение икса и игрика
QVector<float> integerVector; // вектор куда кладём точки (Х и У)
QVector<QPointF> point_for_line; // вектор куда кладём QPointf для line
};
class Krug_qt : public QMainWindow
{
Q_OBJECT
public:
Krug_qt(QWidget *parent = 0);
~Krug_qt();
void krygVertexArray();
void vvodZnach(float R, int kol_toch);
void vvodZnach(float R, int kol_toch, float X, float Y);
void vvodZnach(float R, int kol_toch, int tocka_1, int tocka_2, float X, float Y);
protected:
void paintEvent(QPaintEvent *event);
strKryg _mytKrg; // структура круга
};
#endif // KRUG_QT_H
zvezda.cpp
#include "zvezda.h"
Krug_qt::Krug_qt(QWidget *parent)
: QMainWindow(parent)
{
}
Krug_qt::~Krug_qt()
{
}
void Krug_qt::krygVertexArray()
{
float grad = 360.0/_mytKrg.kol_toch;
float grad_kol_toch = 0.0;
// градусы*M_PI/180 = радианы
int j;
for (j = 0; j < _mytKrg.kol_toch; ++j){
_mytKrg.integerVector.append(_mytKrg.X + (_mytKrg.R * cos(2*sin(1)+M_PI*3)/(2*5))/((cos(2*sin(cos(1*5*grad_kol_toch)))+M_PI*3)/(2*5)));
_mytKrg.integerVector.append(_mytKrg.Y + (_mytKrg.R * sin(2*cos(1)+M_PI*3)/(2*5))/((sin(2*cos(sin(1*5*grad_kol_toch)))+M_PI*3)/(2*5)));
grad_kol_toch = grad_kol_toch + grad;
}
}
void Krug_qt::vvodZnach(float R, int kol_toch)
{
_mytKrg.R = R;
_mytKrg.kol_toch = kol_toch;
_mytKrg.tocka_1 = 0;
_mytKrg.tocka_2 = 0;
_mytKrg.X = 0.0;
_mytKrg.Y = 0.0;
}
void Krug_qt::vvodZnach(float R, int kol_toch, float X, float Y)
{
_mytKrg.R = R;
_mytKrg.kol_toch = kol_toch;
_mytKrg.tocka_1 = 0;
_mytKrg.tocka_2 = 0;
_mytKrg.X = X;
_mytKrg.Y = Y;
}
void Krug_qt::vvodZnach(float R, int kol_toch, int tocka_1, int tocka_2, float X, float Y)
{
_mytKrg.R = R;
_mytKrg.kol_toch = kol_toch;
_mytKrg.tocka_1 = tocka_1;
_mytKrg.tocka_2 = tocka_2;
_mytKrg.X = 0.0;
_mytKrg.Y = 0.0;
}
void Krug_qt::paintEvent(QPaintEvent *event)
{
QPainter painter(this); // Создаём объект отрисовщика
QPen pen_abris(Qt::black, 2, Qt::SolidLine, Qt::FlatCap); // кисть обрисовки (компаса)
painter.setRenderHint(QPainter::Antialiasing); // убираем резкие кубики
painter.setPen(pen_abris); // Устанавливаем кисть обрисовки
vvodZnach(200, 180, 600, 400);
krygVertexArray(); // Набираем массив
int i; bool d_t; int tocka_1; int tocka_2; // используемые переменные
d_t = true; i = 0; tocka_1 =_mytKrg.tocka_1; tocka_2 = _mytKrg.tocka_2; // ТОЧКА ОТРИСОВКИ
for( ; i<_mytKrg.kol_toch; ++i)
{
if(i > tocka_1) // угол "вырезания" начало
{
d_t = false;
if( i < tocka_2) // угол "вырезания" конец
{
tocka_1 = i*2;
d_t = true;
}
}
if(d_t == true)
{
// это отдельно все работает полноценный круг
tocka_2 = tocka_1+1;
painter.drawPoint(QPointF(_mytKrg.integerVector[tocka_1],_mytKrg.integerVector[tocka_2]));
tocka_1 = tocka_1 +2;
qDebug() << "i :"<<i;
qDebug() << "_mytKrg.tocka_1 :"<<_mytKrg.tocka_1;
}
}
}
alas, I can't write on stackoverflow, for some reason they called me maybe because I'm a Russian-speaking man
I'm wondering if it's possible to draw with formulas ?? are there any books or training sites ???
According to the advice of @Homieomorphism. I made changes to the code, but so far I still do not understand how to convert polar coordinates to Cartesian coordinates.
float grad = 360.0/_mytKrg.kol_toch;
float grad_kol_toch = 0.0;
// градусы*M_PI/180 = радианы
int j; float chisl; float znam; float k = 1; float n =5; float m =3;
for (j = 0; j < _mytKrg.kol_toch; ++j)
{
chisl = cos((2*asin(k)+M_PI/180*m)/(2*n));
znam = cos((2*asin(k*cos(n*grad_kol_toch)+M_PI/180))/(2*n));
_mytKrg.integerVector.append(_mytKrg.X + (_mytKrg.R * (chisl/znam) * cos(grad_kol_toch*M_PI/180.0) ));
_mytKrg.integerVector.append(_mytKrg.Y + (_mytKrg.R * (chisl/znam) * sin(grad_kol_toch*M_PI/180.0) ));
grad_kol_toch = grad_kol_toch + grad;
}
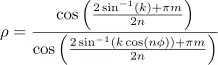


asin(k)in C) , notsin(1)as in your code. – achille hui Nov 01 '21 at 07:32