0

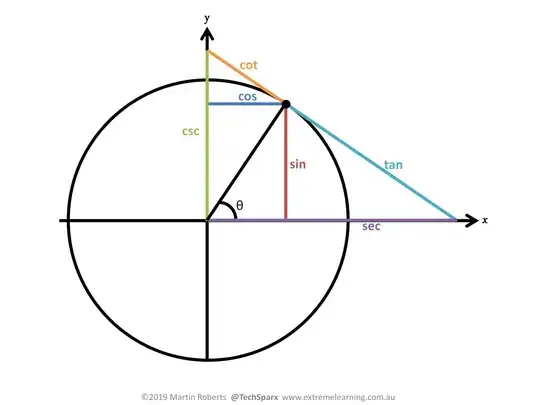
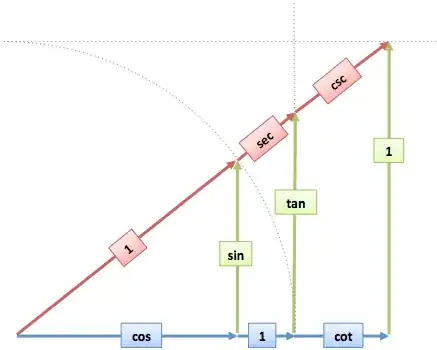
The trigonometric functions $\sin$, $\cos$, $\tan$, $\cot$, $\sec$, and $\csc$, can each be interpreted as the lengths of certain lines in a unit circle. There are generally two collections of interpretations; they are illustrated in the following two pictures: Picture one Picture two

I ask how both the interpretations in picture one, and the interpretations in picture two, can be shown. Note that I do not ask how the functions can be defined in terms of the unit circle, but why these definitions are equivalent to the definitions made using similar triangles (if that was not clear).

Martin Connolly
  • 19
  • Better pictures in https://en.wikipedia.org/wiki/Trigonometric_functions –  Oct 29 '21 at 21:03
  • If you label the radius of the circle as $1$ then you can find each of the triangles in picture 2 somewhere in picture 1. – Ethan Bolker Oct 29 '21 at 21:03
  • Because the lengths are the hypotenuse of right triangles. The lengths (of radii) of the hypotenuse are h. Wikipedia has a very nice explanation when one searches for unit circle + trigonometry. Indeed, @user has posted a picture, but the entry requires actual reading to fully understand. – amWhy Oct 29 '21 at 21:04
  • This is only true in Euclidean geometry, of course some things under certain restraints are going to coincide . What you can do is to look at the proofs of them being the same values – jimjim Oct 29 '21 at 21:06
  • Possible duplicate. – amWhy Oct 29 '21 at 21:08
  • They should have colored the circular arc in pink with the legend $\theta$ as it is the length of this arc. – Gribouillis Oct 29 '21 at 21:29
  • In my opinion, this is a very deep question. In Analytical Geometry, the domain of (for example) the sine and cosine functions are angles, while in Calculus, the domain of the sine and cosine functions are (dimensionless) arc lengths of the unit circle. In "Calculus Vol 1, 2nd Edition" (Tom Apostol, 1966), Apostol specifies axioms that he wants the sine and cosine functions to satisfy. Then, he demonstrates that the typical (Analytical Geometry) definitions of sine and cosine satisfy these axioms as long as the definitions of the domain of these functions are altered in the expected way. – user2661923 Oct 29 '21 at 22:05
  • Surprised that anyone would downvote such a question. I upvoted it from $(-1)$ back to $(0)$. Actually, I would have upvoted it anyway. Per my previous comment, I consider this question deep. – user2661923 Oct 29 '21 at 22:09
  • The question in the title seems different from what you want to ask in the post. Are you actually asking how to show Pic 1 and Pic 2 are equivalent? –  Oct 29 '21 at 22:38

0 Answers0