3

Eliminate $\theta$ from the equations. $$4x=5\cos\theta -\cos 5\theta$$ $$4y=5\sin\theta -\sin 5\theta$$

Alternative forms are

$$x=5\cos^3\theta-4\cos^5\theta$$ $$y=5\sin^3\theta-4\sin^5\theta$$

and $$x=\cos^3\theta(3-2\cos2\theta)$$ $$y=\sin^3\theta(3+2\cos2\theta)$$

Rene Schipperus
  • 39,526
  • 2
    One of the moves you can do in this situation is to go to the exponential forms of $\sin$ and $\cos$ - which sometimes clarifies issues. – Mark Bennet Oct 28 '21 at 21:34
  • 1
    Another approach — which amounts to something close to the exponential form, just in a slightly different shape — is to use the half-tangent substitution to get $x$ and $y$ as rational functions of $t=\tan(\theta/2)$ and then use the usual elimination techniques to get an implicit equation relating $x$ and $y$. – Steven Stadnicki Oct 28 '21 at 22:43

2 Answers2

6

These are the parametric equations of an epicycloid, where the large circle has radius $R=1$, and the smaller exterior rolling circle has radius $r=\frac{1}{4}$.

A possible simplification is writing $$4a=4(x+i y) = 5 z - z^ 5\\ 4b=4(x-i y) = \frac{5}{z} - \frac{1}{z^5}$$ where $z = \cos \theta + i \sin \theta$ and get a relation between $a$, $b$, that implies a relation between $x$ and $y$, see link. Or, we can just give the result provided by WA :

$$-81 - 45 x^2 + 365 x^4 - 15 x^6 - 480 x^8 + 256 x^{10} - 45 y^2 - 2395 x^2 y^2 - 45 x^4 y^2 - 1920 x^6 y^2 + 1280 x^8 y^2 + 365 y^4 - 45 x^2 y^4 - 2880 x^4 y^4 + 2560 x^6 y^4 - 15 y^6 - 1920 x^2 y^6 + 2560 x^4 y^6 - 480 y^8 + 1280 x^2 y^8 + 256 y^{10}=0$$

a curve of degree $10$ 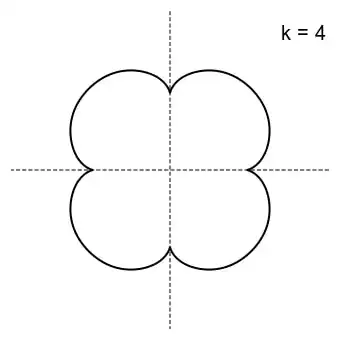epicycloid, <span class=$4$ leaves" />

We can simplify the defining polynomial by writing it as a polynomial in $x^2 + y^2$ and $x^2 y^2$.

$\bf{Added:}$ Following the solution of @ACB: we have the polar representation ($x = r \cos \phi$, $y=r \sin \phi$)

$$\cos^2 2 \phi = \frac{(9 - 4 r^2)(16 r^4+ 3 r^2 + 6)^2}{3125 r^4}= f(r)$$

The function in $r>0$ on RHS is strictly decreasing on $(0, \infty)$. Indeed, we have $$f'(r) = -24\, \frac{(-1 + r^2)^2 (9 + 16 r^2) (6 + 3 r^2 + 16 r^4)}{3125\, r^5}$$ Now, $f(1) = 1$, and $f(\frac{3}{2})=0$. We see that our curve is situated between the circles of radius $1$, and $\frac{3}{2} = 1 + 2\cdot \frac{1}{4}$, as it should.

So now we can write the curve in polar coordinates $$r = f^{-1}(\cos^2 2\phi)$$ where $f^{-1}\colon [0,1]\to [1, \frac{3}{2}]$ is the inverse function of $f$.

orangeskid
  • 53,909
  • There is most likely a form involving fractional exponents such as $(x+y)^{\frac{2}{3}}+(x-y)^{\frac{2}{3}}=1$. – Rene Schipperus Oct 28 '21 at 23:04
  • @Rene Schipperus: That must be the astroid, the small circle rolls inside. But there may be some simpler algebraic form for the curve. Very interesting... – orangeskid Oct 28 '21 at 23:11
  • By various manipulations similar to a previous question I asked with $3$ instead of $5$, I get $x^2+y^2=16w^2+11w+1$ and $x^2y^2=w^3(5+16w)^2$ where $w=\sin^2\theta\cos^2\theta$. One can now divide the quadratic into the quartic getting a linear remainder, and using the quadratic formula, isolate the square root, and squaring, get an algebraic relation. – Rene Schipperus Oct 29 '21 at 00:59
  • @Rene Schipperus: It seems that finding polynomial relations is in some sense a mechanical thing. The astroid has a big polynomial equation, while the algebraic one is quite neat. One can show that the polynomial one implies the algebraic, by making a substitution $x^2=a^3, y^2 = b^3$, in the polynomial, and then factoring (magically, a factor $a+b-1$ appears). It does not seem to work for this curve at hand. Or maybe it works with other substitutions. An interesting curve... – orangeskid Oct 29 '21 at 03:01
  • 1
    Simplifying by hand I got, $3125(x^2-y^2)^2=[9-4(x^2+y^2)][16(x^2+y^2)^2-3(x^2+y^2)+6]^2.$ According to wolfram alpha, the graph looks like this. Any idea? – ACB Oct 29 '21 at 07:36
  • 2
    If you are interested, here's how I reached my solution. (Because I noted my previous comment has been upvoted) – ACB Oct 29 '21 at 11:40
  • @ACB: That is very interesting! And I think it is the right approach, if we don't use a CAS. – orangeskid Oct 29 '21 at 15:25
  • 1
    @ACB Will you publish your calculation as an answer, I will accept it. – Rene Schipperus Oct 29 '21 at 16:19
  • 1
    @ACB : I revised the calculations, your formula is right! ! ( just a - sign off) : $3125 q^2 = (9-4p)(16 p^2 + 3 p +6)^2$, with $q=x^2-y^2$, $p=x^2+y^2$. Wonderful! Please publish your solution! – orangeskid Oct 29 '21 at 16:49
4

Let $c=\cos2\theta$.

$$4x=5\cos\theta -\cos 5\theta\tag1$$ $$4y=5\sin\theta -\sin 5\theta\tag2$$

Squaring and adding ,$$16(x^2+y^2)=25+1-10\cos4\theta$$ $$8(x^2+y^2)=13-5(2c^2-1)$$ $$5c^2=9-4(x^2+y^2)=k$$

Squaring and subtracting, $$16(x^2-y^2)=25\cos2\theta+\cos10\theta-10\cos6\theta$$ $$16(x^2-y^2)=25c+(16c^5-20c^3+5c)-10(4c^3-3c)$$ $$4(x^2-y^2)=c(4c^4-15c^2+15)$$

Substituting $k$, $$100(x^2-y^2)=c(4k^2-75k+375)$$

Further simplifying leads to, $$25(x^2-y^2)=c(16\lambda^2+3\lambda+6)$$ where $\lambda=(x^2+y^2)$.

Squaring again and replacing all values finally we get, $$3125(x^2-y^2)^2=[9-4(x^2+y^2)][16(x^2+y^2)^2+3(x^2+y^2)+6]^2$$

And this is that epicycloid, as being described in @orangeskid's answer!

ACB
  • 3,713
  • Very nice! Somehow there is a sign off, it should be $+ 3(x^2+y^2)$, can you check your calculations? The plot with $+$ seems the correct one. https://www.wolframalpha.com/input/?i=ContourPlot%5B+3125%28x%5E2-y%5E2%29%5E2%3D%3D%289-4%28x%5E2%2By%5E2%29%29%28+16+%28x%5E2%2By%5E2%29%5E2+%2B3+%28x%5E2%2By%5E2%29+%2B6%29%5E2%5D – orangeskid Oct 29 '21 at 16:58
  • 1
    @orangeskid , that was a silly mistake, now corrected. Thanks : ) – ACB Oct 29 '21 at 17:15
  • 1
    Thanks for this solution. Eliminating $\cos 2\theta$ is the key idea. I think this is the canonical answer to the question. – Rene Schipperus Oct 29 '21 at 17:17