7

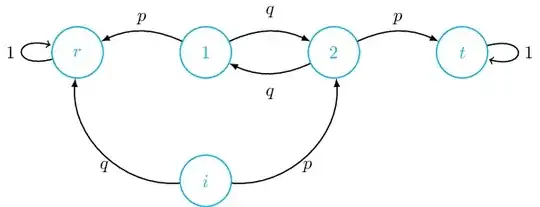
enter image description here

Given the Markov process represented by the above diagram, where the transition probabilites $q$ and $p$ satisfy $p+q=1$. What is the probability $P_r$ of ending up in the sink state $r$, supposing that the initial state is $i$? The answer is

\begin{aligned} P_r &= q+p^2q+p^2q^3+p^2q^5+\dots =q\left[1+p^2\left(1+q^2+q^4+\dots\right)\right] =q\left[1+p^2\sum_{n=0}^\infty q^{2n}\right]\\ &=q\left[1+\frac{p^2}{1-q^2}\right]=\frac{2q}{1+q}, \end{aligned} likewise, what is the probability $P_t$ of ending up in the sink state $t$? The answer is $$ P_t =p^2\left(1+q^2+q^4+\dots\right)=\frac{p^2}{1-q^2}=\frac{1-q}{1+q} $$ Assuming that the transition time between states "1" and "2", in either way, is constant and is given by $\tau$, the transition time from state $i$ to state "2" is also $\tau$, while the other transitions have zero time spans. Hence, the average passage time from state $i$ to state $r$ is given by

\begin{aligned} \bar T_r&= \left(2\tau p^2q+4\tau p^2 q^3+6\tau p^2q^5+\dots\right)/P_r =\frac{2p^2q\tau}{P_r}\sum_{n=0}^\infty(n+1)q^{2n} =p^2(1+q)\tau\left(\sum_{n=0}^\infty nq^{2n}+\sum_{n=0}^\infty q^{2n}\right)\\ &=(1-q)(1-q^2)\tau\left(\frac{q^2}{(1-q^2)^2}+\frac{1}{1-q^2}\right) =(1-q)\tau\left(\frac{q^2}{1-q^2}+1\right) = \frac{\tau}{1+q},\\ \end{aligned}

while the average passage time to state $t$ is given by $$ \bar T_t =\frac{p^2\tau}{P_t}\left(1+3q^2+5q^4+\dots\right)=(1-q^2)\tau\sum_{n=0}^\infty (2n+1)q^{2n}=\frac{(1+q^2)\tau}{1-q^2}, $$ where we have used the following results $$ \sum_{n=0}^\infty q^{2n}=\frac{1}{1-q^2};\qquad \sum_{n=0}^\infty nq^{2n}=\frac{q^2}{\left(1-q^2\right)^2}. $$

The problem with these calculations is that when $q\rightarrow 1$, the average time of capture to state $r$, $\bar T_r$, should go to zero and not to $\tau/2$. I don't know where my mistake(s) is/are.

minmax
  • 877
  • I am confused about this time concept you're talking about. You're basically counting only jumps of the form $1 \to 2$ or $2 \to 1$ in the "average capture time", because all other jumps are "instant"? – Ian Oct 27 '21 at 17:55
  • 1
    Anyway, no, what you are seeing here is a failure to interchange limits. As $q \to 1^-$, the paths from $i$ that don't go directly to $r$ become extremely unlikely ($\Theta(p)$ probability to occur) but also extremely long $\Theta(p^{-1})$ due to the long holding time in ${ 1,2 }$). – Ian Oct 27 '21 at 18:33
  • @Ian besides the jumps from state 1 to 2 and vice-versa, jumps from state i to state 2 also take time $\tau$. – minmax Oct 28 '21 at 01:35
  • Yes, I accounted for that in my answer (current version, not a previous version). – Ian Oct 28 '21 at 01:38

1 Answers1

3

I did not check your actual calculation details, but the intuition for why the expected time to hit $r$ (counting only jumps between $1$ and $2$) does not go to zero as $q \to 1^-$ is as follows.

It is true that the probability that the process going directly to $r$ goes to $1$. But there is still a residual probability $p$ that it doesn't do that. If this happens, the process now spends Geo($p$) time bouncing around in $\{ 1,2 \}$ (which gets longer as $p$ goes to zero), before finally going to either $t$ or $r$.

This means the average time to just absorb at all, counting only jumps between $1$ and $2$ and the jump to $2$, is $q \cdot 0 + p \cdot (1+(p^{-1}-1))\tau=\tau$.

Interestingly this is a case of a failure to obtain convergence in mean from convergence in probability (since the absorption time converges in probability to just zero).

Ian
  • 101,645