I am having some difficulty understanding the rationale that is used to solve the classic calculus problem informally known as The Ladder Around The Corner Problem. In this post, I will propose what I believe is an alternative approach that makes, at least to me, more intuitive sense. I am looking for input as to whether what I am doing is correct...and, in particular, how it varies from the traditional method described below.
The Ladder Around The Corner Problem is framed as:
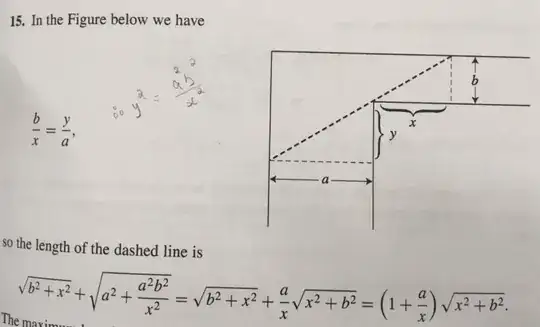
Two hallways, of widths $a$ and $b$, meet at right angles. What is the greatest possible length of a ladder which can be carried horizontally around the corner?
A common derivation can be found here: Intuitive explanation for formula of maximum length of a pipe moving around a corner?
The offending line (i.e. the core concept that makes no sense to me) reads something like:
The maximum length of a ladder which can be carried horizontally around the corner is the minimum length of this dashed line.
...where the "dashed line" is depicted in the below photo:
Fundamentally, I view The Ladder Around The Corner Problem as a variation of The Sliding Ladder Problem with the added constraint of the inner wall corner (i.e. the ladder's physical body, during the act of sliding, cannot move 'beyond' that inner corner).
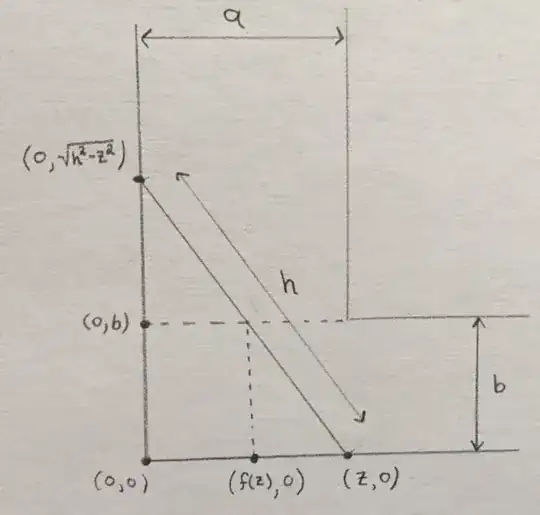
The following picture will be helpful to reference:
The goal is to create a function $f$ that, for a given ladder height $h$ and hallway widths $a,b$, accepts as input a given horizontal distance $z$ that the 'bottom' of the ladder is displaced from the origin and outputs the associated horizontal distance of the latter at the height $b$.
For a given $z$, we can derive the equation of a line that represents the ladder: $y=mx+i$. To solve for the slope and intercept, it is straightforward to confirm that $i=\sqrt{h^2-z^2}$ and $m=\frac{-\sqrt{h^2-z^2}}{z}$. Given this equation, we can solve for what $x$ must be when $y=b$:
$b=\sqrt{h^2-z^2}\left(1-\frac{x}{z}\right)$
Rearranging and simplifying, we have $x=z-\frac{zb}{\sqrt{h^2-z^2}}$
This derivation was for a single $z$, however, we can also use this as the formula for our desired function: $f(z)=z-\frac{zb}{\sqrt{h^2-z^2}}$.
Next, we will take the derivative of this function, which yields $$f'(z)=\frac{\left(h^2-z^2\right)^{\frac{3}{2}}-a^2b}{\left(h^2-z^2\right)^{\frac{3}{2}}}$$
We can solve this for when $f'(z)=0$. This occurs when the numerator equals $0$, which turns out to be when:
$$z=\sqrt{h^2-\sqrt[3]{h^4 b^2}}$$
(although omitted, one can confirm that this is a maximum). We will denote this as $z^*$.
Up to this point, we have not considered the constraint of $a$. To tie this together, consider plugging $z^*$ into $f$.
$f(z^*)$ is effectively telling us the maximum horizontal distance that the ladder will ever attain at a 'height' $b$ above the 'floor' as it slides down the 'vertical' hallway with width $a$ and slides to the 'right' across the 'horizontal' hallway with 'height' $b$.
Importantly, this description is true for any $h, a, $ or $b$ that we choose.
Expanding, we have: $$f(z^*)=\sqrt{h^2-\sqrt[3]{h^4 b^2}}-\frac{\sqrt{h^2-\sqrt[3]{h^4 b^2}}\cdot b}{\sqrt{h^2-\left(\sqrt{h^2-\sqrt[3]{h^4 b^2}}\right)^2}}$$
Throughout this problem, we have only considered a single $f$. However, I think it is reasonable to consider many different $f$'s...each one associated with a different $h$ (a different ladder length). Therefore, for a given $h$, we could think of an $f_h$.
Accordingly, if we set $f_h(z^*)=a$ and solve for $h$, we will know the height of the latter that has, as its maximum horizontal distance at height $b$, the hallway width $a$.
This concept seems crucial, and it is not apparent to me that the classic approach captures this. The movement of the ladder through this hallway combines rotation with translation. In the classic approach, after we determine the length of the ladder, I do not see why we can be certain that the ladder's horizontal displacement at the hallway width $b$ does not increase (which would actually prevent physical movement of the ladder by virtue of impinging against the corner) as we try to rotate + translate it. For my version, however, because our length is determined by considering the maximum horizontal displacement at the hallway width $b$, we can be certain that if we try to move the ladder through translation + rotation, no impingement will occur.
At any rate, I have no clue how to solve the following equation for $h$
$$a=\sqrt{h^2-\sqrt[3]{h^4 b^2}}-\frac{\sqrt{h^2-\sqrt[3]{h^4 b^2}}\cdot b}{\sqrt{h^2-\left(\sqrt{h^2-\sqrt[3]{h^4 b^2}}\right)^2}}$$
I see that we can simplify to:
$$a=\sqrt{h^2-\sqrt[3]{h^4 b^2}}-\frac{\sqrt{h^2-\sqrt[3]{h^4 b^2}}\cdot b}{\sqrt{\sqrt[3]{h^4 b^2}}}$$
If anyone could offer some commentary as to whether my approach is valid and distinct from the classical approach, it would be greatly appreciated.