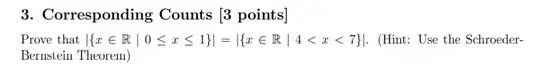The main strategy for these kinds of problems is that you want to show that one set is one-to-one and the other is one-to-one as well. You show this by finding a function the maps from one set to the other.
For this question let's say that the interval $[0,1]$ is $A$, and the other $(4,7)$ is $B$. Showing that $|A| \le |B|$ is saying that this function is one-to-one. To show this:
$[0,1] \mapsto (4,7)$, let's find a function that will map every input from $[0,1]$ to $(4,7)$. A function that would accomplish this would be $f(x) = x + 5$. To show this you could make a simple diagram like: $$0\mapsto5 \\ .5\mapsto5.5\\ \\ \vdots \\1\mapsto6$$
For $(4,7) \mapsto[0,1]$, a potential function could be: $f(x) = \frac{x}{4}-1$. Again, drawing a diagram like: $$5 \mapsto .25 \\ \vdots$$
By showing $[0,1] \mapsto (4,7)$ is one-to-one, then $|[0,1]| \le |(4,7)|$ and have shown $(4,7) \mapsto[0,1]$ meaning $|(4,7)| \le |[0,1]|$ is also one-to-one, then we can conclude using Schröder-Bernstein that $|[0,1]|=|(4,7)|$.