2

The Steiner Ellipse is an ellipse inscribed in a triangle, where the ellipse goes through all three midpoints of the triangle. It is also known as the maximum area inellipse of a triangle.

See here for Marden's Theorem : Link

and here for Siebeck-Marden Theorem : Link.

I'm a highschool student working on the Steiner ellipse, and my team did manage to prove Marden's Theorem and many other stuff for parallelograms in an elementary method, without the use of transformations and stuff.

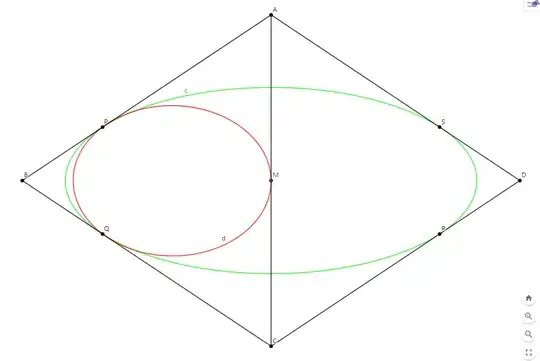
My team is recently working on the expansion of Siebeck-Marden Theorem into parallelograms, and found a conjecture that the ratio of Area(d)/Area(c) is constant. (Picture below : BP : PA = BQ : QC = DS : SA = DR : RC = m : n and M is the midpoint of AC. c is the green ellipse inscribed in ABCD, tangent in P, Q, R, S, and d is the red ellipse inscribed in ABC, tangent in P, Q, M.)

A

We proved that the ratio of the area of the green ellipse and the area of the parallelogram is equal to the following formula : $$\frac{S_c}{S_{ABCD}} = \frac{\pi}{2} \sqrt{k(1-k)}$$

where $k = \frac{n}{m+n}.$ (The formula above is when each side of the parallelogram is internally divided in $1 : k$.)

You can check that this formula does work by letting $k = \frac{1}{2}$; then the ratio becomes $\frac{\pi}{4}$ and this is the Steiner Ellipse for Parallelograms.

The ratio seems to result in $\frac{2}{3 \sqrt{3}}$ by guess, and we checked for 5 different cases in Geogebra.

$$\text{Ratio} = \frac{\text{Area}(c)}{\text{Area}(d)} \approx 0.39$$

The result is not that correct since we did not construct the ellipse, but drew it by hand(which is an approximation.). The result is still very close to the guess.

Is there a paper about these expansions into parallelograms? I found Alan Horwitz's work though. Also since we're working on a paper, it would be better if paper proofs or hints are exhibited. (It is quite difficult to put an answer in a Q&A site as reference, and it is immoral to offer as if I proved it.)

This is just a guess, so it might be false if computed correctly. Any help would be appreciated.

Jean Marie
  • 81,803
Vue
  • 1,375
  • See another article similar to your second reference. – Jean Marie Oct 21 '21 at 09:39
  • Two questions : 1) How are defined variables c and d in S(c)/S(d) ? 2) You say "parallelogram" but your figure displays the particular case of a lozenge. Isn't it misleading ? Couldn't you replace this figure by a more general one ? – Jean Marie Oct 21 '21 at 09:45
  • Another well-written AMM text using barycentric coordinates, a key technique I advise you to consider for such questions using ratio of areas. – Jean Marie Oct 21 '21 at 09:54
  • Reference to Alan Horwitz's paper. – Jean Marie Oct 21 '21 at 09:59
  • @JeanMarie 1. S is the area function and c and d are ellipses in the picture. (explanation added) 2. I drew a lozenge since it was easier to draw, but I did check other 5 cases in a parallelogram. Will change the picture though. – Vue Oct 21 '21 at 11:44
  • @JeanMarie Thanks, but I have already read those papers; am I missing something? I am curious about the area of an ellipse tangent in one midpoint and two m:n internally dividing points. Also - me and my team members no literally nothing about barycentric coordinates; I'm looking forward of an elementary proof. Thanks again for the idea, but we do not have enough skill and experience to use it. – Vue Oct 21 '21 at 11:48
  • You could find useful this old answer of mine: https://math.stackexchange.com/questions/1465346/calculation-method-for-a-british-standard-based-on-finding-an-ellipse-given-tang/1466276#1466276 – Intelligenti pauca Oct 21 '21 at 12:24
  • @Intelligentipauca How would that work in this case? – Vue Oct 21 '21 at 13:10
  • That rule will allow you to compute the lengths of the axes (or conjugate diameters) of both ellipses. – Intelligenti pauca Oct 21 '21 at 14:09
  • I have taken the liberty to remove the fourth graphic which was only containing a formula moreover with Korean characters (I have nothing against Korean characters but it is always better to be clear for the majority of readers). – Jean Marie Oct 21 '21 at 19:55

1 Answers1

1

Let $N$ be the midpoint of $PQ$. Then: $MN:BN=n:m$ and $PN:AM=m:(m+n)$.

We can use the following useful property of ellipses:

If from an external point $B$ a pair of tangents $BP$, $BQ$ are drawn to an ellipse of centre $M$, and line $BM$ intersects $PQ$ in $N$ and the ellipse in $G$, then $N$ is the midpoint of $PQ$ and $MG$ is the mean proportional between $MB$ and $MN$.

This property is easy to prove for a circle, and still holds for an ellipse because a stretching preserves all ratios on the same line.

With this property we can find $MG/MB$, $MH/MA$ and $OE/MB$.

Finally, from ellipse equation $(PN/OF)^2+(ON/OE)^2=1$, we can find $OF/MA$.

The ratio of areas is $(OE\cdot OF)/(MG\cdot MH)$ and, according to the result I got, is not independent of $m/n$.

Ask for further details, if needed.

enter image description here

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77