0

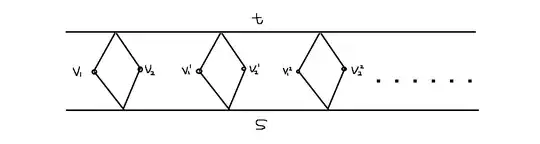
For a graph $G(V, E)$ embedded in the 2-sphere $S_2$, $V=\{s, t, v_1, v_2\}$, $s$ and $t$ are located at the two poles of the $S_2$. There exists two paths $sv_1t$, $sv_2t$ in $G$. Now we have a surface $U$ obtained in the following way:

  1. Cut out holes in $S_2$ at $s$ and $t$. This transforms the sphere into a cylinder where the boundaries or holes at the ends are identified with $s$ and $t$.
  2. Make a cut from one end of the cylinder to the other to obtain a rectangle.
  3. Taking an infinite number of copies of this rectangle and glueing them together to form an infinitely long strip (surface $U$) whose two boundaries are again identified with the nodes $s$ and $t$.

Is U the universal covering surface of $S_2\backslash\{s, t\}$? If so, does U look like the one drawn below?

enter image description here

YiYuanzhe
  • 21
  • 1
    Sphere minus a point is homeorphic to 2-plane and removing another point is same as removing on point from 2-plane. – C.F.G Oct 20 '21 at 11:56
  • 4
    You space is homeomorphic to $S^1\times \mathbb R$, whose universal cover is $\mathbb R\times \mathbb R$ where the first map is the universal cover $\mathbb R\to S^1$ and the second map is the identity. – Pedro Oct 20 '21 at 12:23

1 Answers1

0

As Pedro mentions in the comments, the complex plane with euclidean topology is the universal covering space of $S^2\setminus\{v_1,v_2\}$. For an explicit covering map consider the exponential map $$\operatorname{exp}\colon \mathbb{C}\rightarrow \mathbb{C}\setminus\{0\}\cong \overline{\mathbb{C}}\setminus\{0,\infty\}\cong S^2\setminus\{v_1,v_2\}.$$ Here, we identify $S^2$ with the one-point compactification $\overline{\mathbb{C}}$ of $\mathbb{C}$ via stereographic projection. Similarly, we identify $v_1\in S^2$ with $0\in\overline{\mathbb{C}}$ and $v_2\in S^2$ with $\infty\in\overline{\mathbb{C}}.$ If you identify $v_1$ and $v_2$ with different points of $\overline{\mathbb{C}}$, you can construct a covering map $\mathbb{C}\rightarrow S^2\setminus\{v_1,v_2\}$ by composing the exponential function with a suitable Möbius transformation (i.e., an automorphism of the Riemann sphere). For an example, see my answer here, for instance.

Since I am not sure what you mean by "taking an infinite number of copies of this rectangle and glueing them together" (i.e. how do you glue?), I cannot answer whether your space $U$ is the universal covering space of $S^2\setminus\{v_1,v_2\}$.

Max Demirdilek
  • 3,018