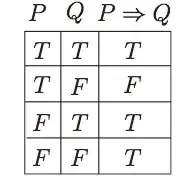
In logic, implication refers to the following truth table. Initially, we can't know if an implication is true or false if all combinations of $P$ and $Q$ are possible.
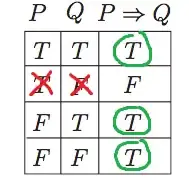
Let's imagine we've ruled out the possibility that $Q$ is false when $P$ is true. From the truth table, we can see that the implication is true. This matches my real-world intuition.
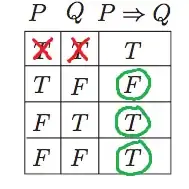
But let's imagine a different scenario: we've ruled out the possibility for $Q$ to be true when $P$ is true. My intuition would say that the implication is now most definitely false. However, according to the truth table, we haven't learnt anything about the implication. It is still either true or false.
Clearly there is a discrepancy between my "intuitive" implication, and the version of implication defined in logic. I will call my implication "traditional implication".
Traditional implication would be defined as true if the logical implication is a tautology, otherwise false. (It can only be a tautology if we've ruled out the second row, i.e. $P \land \lnot Q$ is impossible)
From what I know, traditional implication is what's used to test the validity of an argument, as opposed to logical implication. Am I right in saying this? (I'm pretty sure this is correct).
Is there any such operation in logic that represents traditional implication? Is there any symbol for it? Is there a clean way of writing down this type of implication? Or do I have to resort to using the following, which is quite messy, and possibly incorrect?
$$\forall p, q (p \implies q)$$
Edit: I just came across tautological implication and tautological consequence. Hopefully this is related to what I'm talking about, which I'm reading up on now.