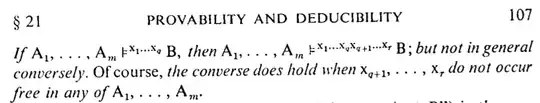2

Mathematical Logic by Kleene page 107

enter image description here

As I understand for one variable $\forall x.A(x)$ it means that instead of considering all possible logical functions for $A(x)$ we need to choose only the function $I(x)=true$ for all values of $x$.

$A_1,...,A_m\models^{x_1...x_q}B \equiv \forall {x_1,...,x_q}.A_1,...\forall {x_1,...,x_q}.A_m \models B$ - if I got it right.

I see no difference between $\forall{x,y}.A(x,y)$ and $\forall{x}.A(x,y)$ because logical function $I(x,y)$ for $\forall{x}.A(x,y)$ always $true$ regardless of $y$ and the same holds for $\forall{x,y}.A(x,y)$

I can't get the difference between $A_1,...,A_m\models^{x_1...x_q}B$ and $A_1,...,A_m\models^{x_1...x_qx_{q+1}...x_r}B$

user142248
  • 61
  • It should be clear that $\forall x,y.A(x,y)$ and $\forall x. A(x,y)$ ought to mean different things - for example, if $A(x,y)$ is $y\le x$, then $\forall x,y.A(x,y)$ should be false in $\mathbb{N}$ with $\le$ interpreted in the obvious way but $\forall x. A(x,y)$ will be true for one particular variable assignment (namely $y\mapsto 0$ or $y\mapsto 1$, depending on whether you consider $0$ a natural number). Keeping this in mind should help isolate the formal point of difference. – Noah Schweber Oct 16 '21 at 02:18
  • So $\forall x.A(x,y)$ means $\forall x\exists y.A(x,y)$ – user142248 Oct 16 '21 at 04:10
  • 1
    No, it doesn't mean that either. Both "$\forall x,y. A(x,y)$" and "$\forall x\exists y. A(x,y)$" are sentences (or closed formulas): their truth value is determined as soon as a model is specified. The truth value of the formula "$\forall x. A(x,y)$" is not in general determined by the model alone; we also need to know a variable assignment for $y$. Think of a formula with free variables as defining a subset of (some Cartesian power of) the structure in question. – Noah Schweber Oct 16 '21 at 04:16
  • Kleene's old superscript-variable notation denotes closure of all universal quantifiers binding each superscript-variable applicable for each premise $A_i$, it's a little confusing but you should regard it as a closed formula by all applicable universal quantifiers. – cinch Oct 16 '21 at 04:21
  • Sorry, I didn't get you. Model: $B={1,2,3}, I(1,2)=I(2,1)=I(3,3)=I(3,1) = true$ other pairs are $false$, so $\forall x$ there $\exists y$. Could you please provide some examples for the difference between $∀x.A(x,y)$ and $∀x∃y.A(x,y)$? – user142248 Oct 16 '21 at 05:42
  • If your $A(x,y)$ is $y≤x$, then we should have $I(1,1)=I(2,1)=I(3,1)=I(2,2)=I(3,2)=I(3,3)=true$ and other combos false to arrive at your conclusion $\forall x \exists y.A(x,y)$. As for $\forall x.A(x,y)$ it's an open formula with $y$ free as a parameter, so it hasn't any truth value. Kleene meant $\forall x \forall y.A(x,y)$ by default to close all superscript-variable as sentences... – cinch Oct 16 '21 at 20:20
  • In my understanding $A(x,y,z),\forall x.A(x,y,z),\forall x\forall y.A(x,y,z)$ are predicate variables each of them determines a set of logical functions that are applicable to them. How can I determine those sets to compere different forms of $A(x,y,z)$ (with or without quantifiers)? For example, consider $\forall x \forall y.A(x,y,z)$ form, whether the logical function that gives $true$ for every $y$ regardless of $x,z$ satisfies that form for $x,y,z\in{0,1}$ domain? – user142248 Oct 17 '21 at 10:05

0 Answers0