5

$$x=\sqrt{2x+3}$$

If you solved this traditionally you would get $x_1=3$ & $x_2=-1$. But inputting $x=-1$ in $\sqrt{2x+3}$ gives $+1$ or $-1$. The original equation is only valid if $\sqrt{2x+3}=-1$. So does $x=-1$ technically count as a solution or not?

ShootinLemons
  • 187
  • 5
    notice that $\sqrt{1}$ is not "+1 or -1". It's only 1. The square root is a single-branch function. Also notice that, when doing the "traditional way", you have to assume $2x+3\geq 0$. Therefore, we already rule out $x=-1$. – Matti P. Oct 11 '21 at 10:09
  • Related: https://math.stackexchange.com/questions/4260843/how-to-solve-for-x-without-squaring – lone student Oct 11 '21 at 12:45
  • 1
    Convention is that the square root is always the non-negative alternative, hence $-1$ is no solution. – Peter Oct 11 '21 at 16:53
  • 1
    Yes , if the equation is satisfied then it is a solution. If a value makes the equation to be correct what else can it be but a solution ? – jimjim Oct 11 '21 at 22:42
  • 1
    @MattiP. but the condition $2x+3 \ge 0$ is satisfied when $x=-1$. $2\cdot-1+3=-2+3=1$. I don't get your point. – ShootinLemons Oct 12 '21 at 06:09

4 Answers4

6

If you substitute it back in the original equation and it does not work, it is not a solution.

$$ a = b \Longrightarrow a^2=b^2$$

but

$$a^2 = b^2 \not \!\!\! \implies a = b.$$

PierreCarre
  • 20,974
  • 1
  • 18
  • 34
  • This is not what my question is about, I knew this already. My question is in regard to this specific case where depending on whether you take the negative or positive root of the radical, you can satisfy the original equation. Let $y=\sqrt{1}$ this implies that $y=\pm1$. Now let $P:y=y^2$. $P$ is only true for one of the roots of $y$ so convention would say the only solutions to $P$ is $y=1$. My original problem is similar to this, but a bit more complicated. – ShootinLemons Oct 12 '21 at 06:54
  • @ShootinLemons I do think I answered your question... When you use $\sqrt{\cdot}$ in an equation, unless stated otherwise, you are referring to a real function $f:\mathbb{R}_0^+\to \mathbb{R}_0^+$, which is one-to-one. – PierreCarre Oct 12 '21 at 08:12
3

$$x=\sqrt{2x+3}$$

If you solved this traditionally you would get $x_1=3$ & $x_2=-1$.

  • Untrue; the so-called “traditional” solution is this: $$x=\sqrt{2x+3}\tag{*}$$$$\implies x^2=2x+3\\\implies x=-1\,\text{ or }\,3;\\\text{of the two }\textbf{candidate solutions},\text{ $-1$ doesn't actually satisfy (*), so $x=3$ is its only solution}.$$

    (The fact that $\;x^2=2x+3\kern.6em\not\kern-.6em\implies x=\sqrt{2x+3}\;$ created an extraneous solution in the first step.)

  • Here's an alternative correct solution (the above is usual and preferable): \begin{align}&&x&=\sqrt{2x+3}\\&\iff &x^2&=|2x+3|\\&&&= 2x+3\;\text{ or }\,-2x-3\\&\iff&x&=-1\,\text{ or }\,3.\end{align}

ryang
  • 38,879
  • 14
  • 81
  • 179
2

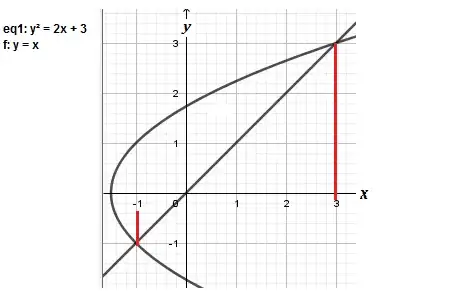
In real analysis, the answer is definitely no. Square roots must be nonnegative. They must be additively inverted (meaning they take a negative sign) to access the negative root, so in this case $x=-1$ would solve $x=-\sqrt{2x+3}$ instead of $x=\sqrt{2x+3}$.

This answer explores the possibilities offered by other domains.

Complex analysis

In the complex domain the square root function has two branches that connect continuously to each other rather than directly back to the same branch, as if you were riding a Möbius strip. You could indeed find a negative root with a properly defined branch of the function.

However, we typically define a principal branch such that the real part of the square root is always nonnegative and, where that is zero, the imaginary part is chosen to be nonnegative. This precludes reaching $x=-1$ in the original equation,or roots involving negative "square roots" of real numbers generally, unless we depart from the standard definition even in the complex domain.

$p$-adics

This case is a little more interesting. Consider the familiar Maclaurin series

$\sqrt{1+x}=1+\frac12x-\frac18x^2+...$

which, in real analysis, properly gives a nonnegative value whenever the sum converges ($|x|<1$). We can carry this over into $p$-adics and, where the series converges,we may define a principal square root as the sum thereby chosen. Where the radicand $1+x$ is a rational square, this sum could indeed correspond to what would be the negative root in real analysis. For instance, in $2$-adics the square root of $9=1+8$ obtained from the series is $-3$.

In the problem at hand we ask whether $-1$ can be obtained as a square root in this way. That answer is no; the series for $\sqrt{1+0}$ always converges trivially to $+1$. In $2$-adics where the Maclaurin series converges, we still find that only $x=3$ matches with the sum of the series when checked against $x=\sqrt{2x+3}$.

But other negative integer roots could potentially be obtained. Suppose we were to consider instead the equation

$x=\sqrt{2x+8}$

whose apparent roots, after squaring and solving the resulting quadratic equation, are $-2$ and $4$. The radicand is respectively $4$ and $16$ for these candidates. In real analysis only $x=4$ passes muster. But if instead we choose the $3$-adic domain, then both $4-1=3$ and $16-1=15$ have a terminal zero which is sufficient for the Maclaurin series for $\sqrt{1+x}$ to converge. We may then check $x=-2$ and $x=4$ against the $3$-adic sum of the Maclaurin series, and now we find that they both match: $\sqrt{1+3}$ converges to $-2$ and $\sqrt{1+15}$ converges to $+4$. Thus in $3$-adics, unlike in the reals, both $x=-2$ and $x=4$ may be deemed solutions of $x=\sqrt{2x+8}$ with the Maclaurin-series based square roots.

Oscar Lanzi
  • 39,403
-1

The sign in front of a radical is $\pm$ presents itself with symbolic action detail whether or not intended.

Solution of equations

$$ y=x, \; y^2= 2x + 3\; $$

have two intersections

$$ (-1,-1),(3,3)$$

would present themselves due to association with all connotations of the symbol's action.. represented by the square root radical in this case.

enter image description here

If technically is meant to include comprehensively , yes, it does count as a valid solution.

EDIT1:

Let us hypothetically assume that you or another OP asked the question like this:

$$x=-\sqrt{2x+3}$$

If you solved this traditionally you would get $x_1=-1$ & $x_2=-3$. But inputting $x=3$ in $\sqrt{2x+3}$ gives $+3$ or $-3$. The original equation is only valid if $\sqrt{2x+3}=-3$. So does $x=+3 $ technically count as a solution or not?

As you can guess my answer would be exactly on the same lines.

Narasimham
  • 40,495
  • I think this approach is more confusing then useful. You are attributing a meaning to the symbol $\sqrt{\cdot}$ and that is just fine, but you must agree that saying that for most purposes you consider$$\sqrt{\cdot}: \mathbb{R}_0^+ \to \mathbb{R}_0^+.$$When you ask someone the the square root of $4$ you are not expecting people to say "well, it can be -2". – PierreCarre Oct 11 '21 at 13:37
  • As far as I understood the question it is about a fuller technical inclusion, how the second root gets unwittingly roped in, and if there are circumstances where the seemingly extraneous root makes some sense. – Narasimham Oct 11 '21 at 14:08
  • When the other root makes sense, for example in the usual formula for the solution of a quadratic equation, the usual practice is to write $\pm \sqrt{\phantom{0}}.$ So there is no need to cause confusion by making two definitions for the $\sqrt{\phantom{0}}$ symbol. – David K Oct 11 '21 at 18:42