Too long for a comment
Let's consider a general case:
$$I(m,k)=\int_{0}^{\infty}\frac{x^{m}}{1 + x^k}dx; \,\,m\in (-1;k-2)$$
Then $$\int_{0}^{\infty}\frac{x^{n}}{1 + x^{2n}}dx=I(n,2n)$$
I would recommend to make substitution in the integral first:
$$I(m,k)= (t=x^k)\,\,\frac{1}{k}\int_0^\infty\frac{t^{\frac{m+1}{k}-1}}{1+t}dt$$
Then we can easily evaluate the integral via Beta function, or using complex integration:
$$I(m,k)= (x=\frac{1}{1+t})\,\,\frac{1}{k}\int_0^1 x^{-\frac{m+1}{k}}(1-x)^{\frac{m+1}{k}-1}dx$$
$$=\frac{1}{k}B\Big(1-\frac{m+1}{k};\frac{m+1}{k}\Big)=\frac{\Gamma(1-\frac{m+1}{k})\Gamma(\frac{m+1}{k})}{k}=\frac{\pi}{k}\,\frac{1}{\sin\frac{\pi(m+1)}{k}}$$
$$I(n;2n)=\frac{\pi}{2n}\frac{1}{\sin\frac{\pi(n+1)}{2n}}=\frac{\pi}{2n}\frac{1}{\cos\frac{\pi}{2n}}$$
If we want to use the complex integration to evaluate $I(m,k)$, we can integrate along the keyhole contour with the cut $[0;\infty]$:
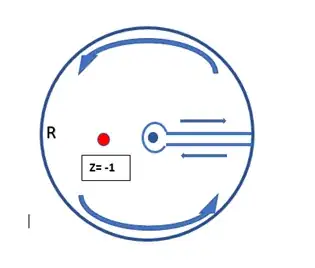
Let's denote $a=\frac{m+1}{k}-1\,\, (a<0)$, then
$$\frac{1}{k}\oint\frac{z^a}{1+z}dz=I(m,k)-e^{2\pi ia}I(m,k)=2\pi iRes_{z=e^{\pi i}}\frac{1}{k}\frac{z^a}{1+z}$$
$$I(m,k)=-\frac{\pi}{k}\frac{1}{\sin \pi a}=\frac{\pi}{k}\,\frac{1}{\sin\frac{\pi(m+1)}{k}}$$
