0

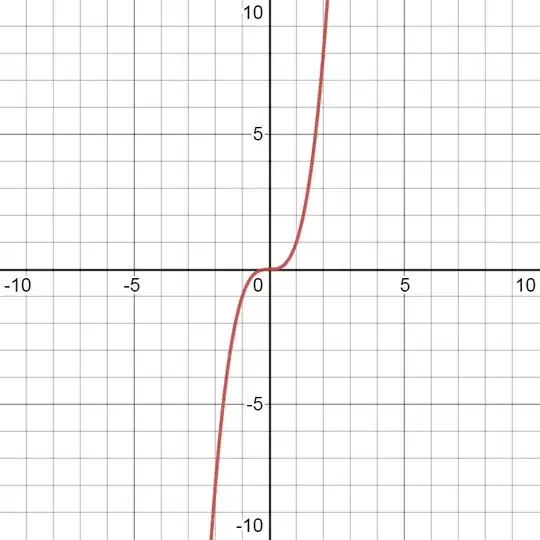
Consider the graph of $f(x)=x^3$:

enter image description here

The slope of the above graph is constantly changing: each point of the graph has a different slope. Now, the question arises, how do we find the slope of a point? We can't use the slope formula to calculate it because we get an indeterminate form: $\frac{f(x)-f(x)}{0}=\frac{0}{0}$.

Let us consider 2 different points $A$ & $B$ of the above graph. Now, if we find the slope of the secant line $AB$, it'll be an approximation of the slope of $A$. If we pick a point that is closer to $A$ than $B$, $C$, the slope of $AC$ will be a better approximation of $A$'s slope. Now, if we know what the value is that the slopes of the secant lines are approaching as the points are getting closer and closer to $A$, we will be able to find the best approximation and the most correct answer of the slope of that point: the approached value. It is the best approximation because we know that the approximations are getting better and better as the approximations are getting closer and closer to the approached value, so the approached value is the most accurate approximation, and it is the slope of the point. We can calculate this approached value by taking the limit:

$$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$$

$f'(x)$ is the approached valued, and it is known as the derivative of $f$ at $x$.

Question:

  1. Is my understanding of derivatives correct?
tryingtobeastoic
  • 3,176

1 Answers1

1

Yes.

Another useful formula is the Weierstraß definition: $$ \mathbf{f(x_{0}+v)=f(x_{0})+J_{x_0}(v)+r(v)} $$ where $v$ is the direction of the derivative (the $x$-axis in your case), $J_{x_0}(v)=f'(x_0)\cdot v$ is a linear map (which assigns the direction to the slope at point $x_0$, the actual derivative), and $r(v)$ an error function such that $\lim_{v \rightarrow 0}\frac{r(v)}{\|v\|}=0$ (means it goes faster to zero than linear).

The advantage of this formula is, that it works in all dimensions and that it shows the various viewpoints one can (and later on, e.g. in physics) will have on a derivative.

Marius S.L.
  • 2,245