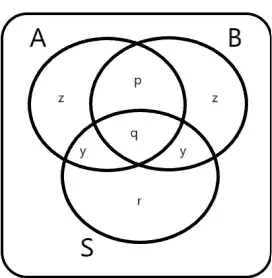
Let $A, B$ be independent events, and assume we also know the probabilities $P(A\mid S)=P(B\mid S)=c_{is}$, and of $P(A\mid \bar S)=P(B\mid \bar S)=c_{i\bar s}$ and $P(S)=c_s$.
how would we find $P(A,B\mid S)$ ?
My idea was to rewrite $P(A,B | S)= P(A | S,B) P(B|S)$, and then $P(A | S,B)=P(A|S)$... however, my last equality is not true.
N.B. This does not Answer the Question, but it's impossible to post as a comment, so here goes:
Additionally, since events $A$ and $B$ are independent, $\;(y+z)^2=(p+q)(1-p-q-2y-2z).$
$$P(A,B\;|S)\\=\frac q{q+r+2y}\\=\frac {c_{is}c_s-y}{c_s}.$$
This is the closest that I got to your request. If I've made any error, let me know and I will edit/delete this Answer.
