3

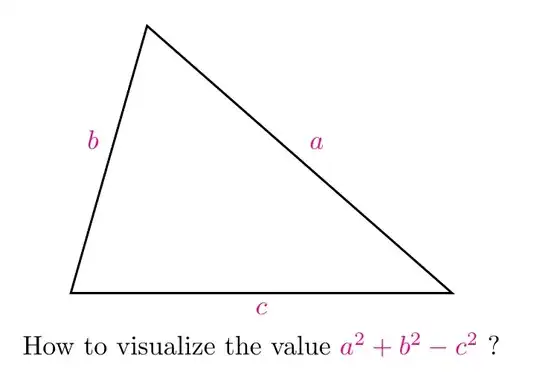
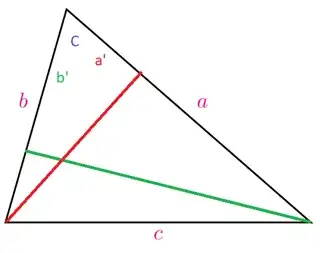
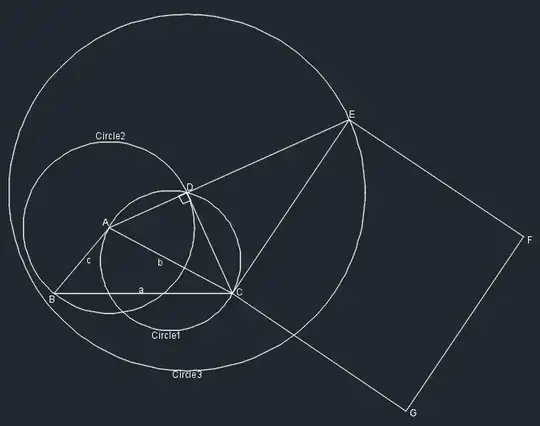
Let $a$, $b$, and $c$ be three lengths of sides of a triangle, that is, $a+b>c$.

How can we visualize the value $a^2+b^2-c^2$ as length of some segment or area, ... constructed from the triangle $ABC$ ?

The value appears in some context, for example Law of Cosine, barycentric coordinate of orthocenter.

I searched, and tried myself for a while, but still have no clues.

enter image description here

Black Mild
  • 274
  • 1
    It is impossible to find a segment of length $a^2 + b^2 - c^2$ because (by dimensional arguments) these are AREAS, not LENGTHS. – David G. Stork Oct 04 '21 at 06:16
  • 2
    @DavidG.Stork $a^2+b^2-c^2$ can be attained by straightedge and compass construction. So even if this has not the dimension of a length, it is absolutely possible to have a segment with $a^2+b^2-c^2$ length with usual constructions. – mathcounterexamples.net Oct 04 '21 at 06:31
  • Thanks for comments! My question is visualizing,no matter on length or area, .... (see my update) – Black Mild Oct 04 '21 at 07:01
  • 1
    See my answer here. – Blue Oct 04 '21 at 10:57
  • @mathcounterexamples: Nope. Constructing a region with AREA $a^2 + b^2 - c^2$ by straightedge and compass construction is NOT the original problem asked. You state "...it is absolutely possible to have a segment..." If so, show it. (Certainly your link to straightedge and compass construction does NOT.). The OP changed the question to "length or some AREA...". But you said "segment." So show it. – David G. Stork Oct 04 '21 at 12:28
  • @DavidG.Stork Come on! It is a trivial result of straightedge and compass construction that for any segments of lengths $r,s \in \mathbb R$, a segment of length $r \cdot s$ is constructible. This link provides you with a construction. So for $a$, you can build a segment of length $a^2$. And then $a^2+b^2-c^2$ trivially follows. – mathcounterexamples.net Oct 04 '21 at 12:36
  • @mathcounterexamples.net: To be a bit more precise, a segment of $r\cdot s$ is constructible from segments of length $r$, $s$, and $1$. Without the unit segment, you're stuck. – Blue Oct 04 '21 at 12:43
  • @Blue For sure! But how can you speak of a length equal to the real $a$ if you don't know what $1$ is??? – mathcounterexamples.net Oct 04 '21 at 12:44
  • @mathcounterexamples.net: Assigning real values to lengths isn't necessarily a requirement for geometric constructions. For example, the Pythagorean Theorem $a^2+b^2=c^2$ is true by construction regardless of how one chooses the unit length. – Blue Oct 04 '21 at 12:48
  • @Blue I also agree with that... But the question is how to visualize $a^2+b^2-c^2$? So you need to build something that has the measure of that number. – mathcounterexamples.net Oct 04 '21 at 13:11
  • @mathcounterexamples.net: I wasn't addressing the question, just the oversight in your comment. ... As to the question, you'd have to introduce a unit segment to the figure to construct a segment of length $a^2+b^2-c^2$. This is not-unreasonable (especially if there's a way to work the segment into the figure itself, as opposed to just using it to performing construction "off to the side"), but it may not be OP's intention. ... Anyway, it wasn't my intention to get into a big discussion about this, so this will be my final comment. Cheers! – Blue Oct 04 '21 at 13:42

4 Answers4

2

law of cosines

The law of cosines is:

$$a^2+b^2=c^2+2ab\cos C$$

$ab\cos C$ is the dot product of the vectors $\vec a$ and $\vec b$.

It therefore says that:

$$c^2=(a')^2+(b')^2$$

JMP
  • 21,771
2

Here is one way of doing a construction to illustrate the area $a^2+b^2-c^2$:

From the Cosine Rule we know this quantity is equivalent to $2ab\cos C$.

Therefore at $C$ draw a line $CD$ perpendicular to $CA$ and of length $b$, so that $\angle BCD=90-C$.

Now draw a perpendicular from $D$ onto $BC$ (which has length $a$), meeting $BC$ at $E$. The line $DE$ has length $b\cos C$.

Finally you can construct a rectangle whose base is BC and height is $2\times DE$, and this rectangle has the required area.

David Quinn
  • 34,121
1

It represents work or energy experienced rather than what can be seen as a pure geometric quantity.

From Cosine Rule

$$ a^2+b^2-c^2 = 2ab \cos C \;$$

This is the work done by force a when displaced through distance 2 b. For example no work done by a person walking on frictionless ground as the vectors are perpendicular and dot product is zero.

enter image description here

Narasimham
  • 40,495
  • 1
    Let's just note that you haven't shown a segment with LENGTH $a^2 + b^2 - c^2$, the original problem. (The OP later changed the problem to include area... fine.) – David G. Stork Oct 04 '21 at 12:31
1

enter image description here

Here is one possible geometric construction:

  1. Draw $Circle1$ with diameter $AC$.
  2. Draw $Circle2$ with center $A$ and radius $c$. Let $Circle2$ intersect $Circle1$ at $D$
  3. Draw $Circle3$ with center $D$ and radius $a$.
  4. Extend $AD$ to meet $Circle3$ at $E$.
  5. Construct square $CEFG$.

As an exercise, calculate the area of the square $CEFG$.

Saeed
  • 1,872