0

When I first looked at the construction of natural numbers the Peano axioms were shown as a way to do this, without the need of anything else, in the way described in this video and Analysis I by Terence Tao. The Peano axioms were described as agnostic on the subject of what $0$ or the successor function was. Then I saw that you could use $0=\emptyset$ and $S(n) = \{n\}$ to get the Zermelo ordinals and $S(n) = n \cup \{n\} $ to get the von Neumann ordinals.

However, then I saw that you can use the ZF axioms, like the axiom of infinity, and VN ordinals to construct the natural numbers as shown here and here. Here the natural numbers were constructed without the Peano Axioms, instead the Peano axioms were shown as a theorem describing the properties of the natural numbers instead of axioms that construct them. 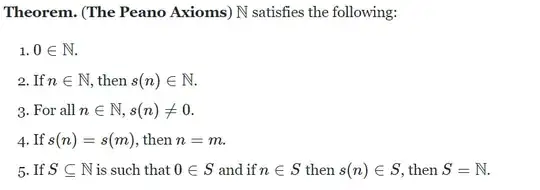enter image description here Does this mean that the Peano axioms aren't axioms?

user716881
  • 191

1 Answers1

2

Whether a given logical statement is an axiom or theorem isn't something inherent to the logical statement, it depends on how you're using it. In this case, yes, the Peano axioms are playing the role of a theorem (something that's proved).

But the Peano axioms are also valuable as axioms (something to prove stuff from).

Take for instance, the axiom of choice, Zorn's lemma, and the well-ordering principle. Any one of these could be used as part of an axiom system to prove the other two, so which one is an axiom depends on this choice.

TomKern
  • 2,977