Complementary Trigonometric relationship for sine and cosine

Question

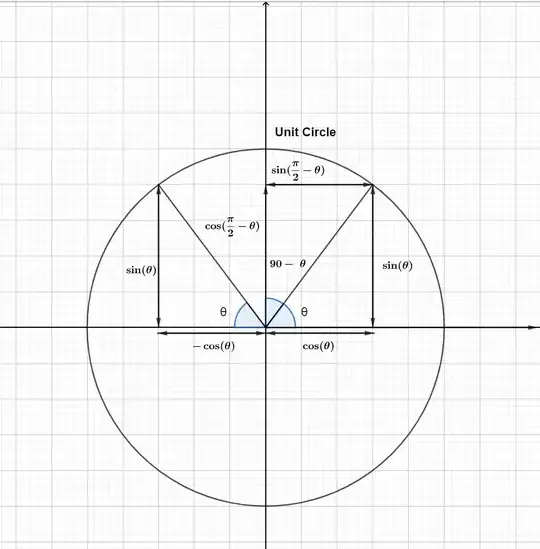
To begin, let's start with the first quadrant in the unit circle:

It's easy to see why(due to complementary angles):

$$\cos\left(\frac{\pi}{2}-\theta\right) = \sin(\theta)$$ $$\sin\left(\frac{\pi}{2}-\theta\right) = \cos(\theta)$$

But what about Quadrant 2, 3 and 4, how do I visualise and prove these using the unit circle?

Q2: $$\sin\left(\frac{\pi}{2}+\theta\right) = ???$$ $$\cos\left(\frac{\pi}{2}+\theta\right) = ???$$

Q3:

$$\sin\left(\frac{3\pi}{2}-\theta\right) = ???$$ $$\cos\left(\frac{3\pi}{2}-\theta\right) = ???$$

Q4:

$$\sin\left(\frac{3\pi}{2}+\theta\right) = ???$$ $$\cos\left(\frac{3\pi}{2}+\theta\right) = ???$$