$10$ circles ($2$ large of radius $R$, $6$ small of radius $r$ and 2 small of radius $t$) are enclosed in a square. How we find $r$ in terms of $t$?

Question

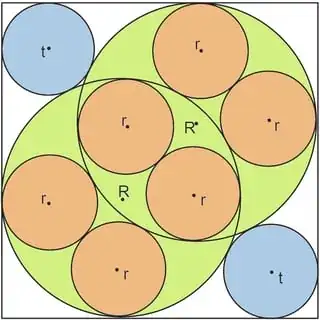
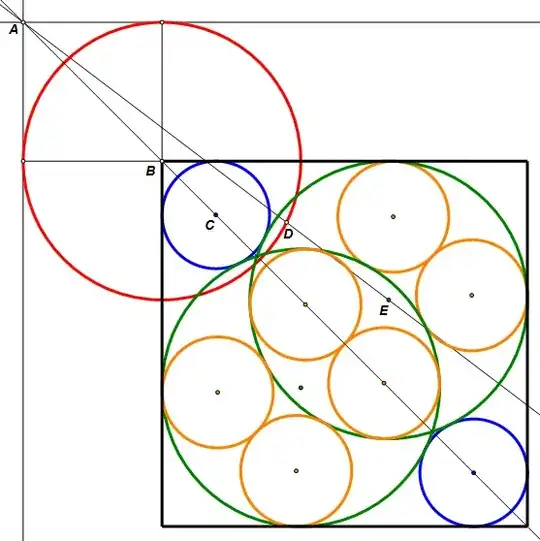
Let us embed $2$ large intersecting circles of radius $R$ into a square as depicted by the figure below. These two circles are highlighted green. Into these $2$ circles we embedd $6$ smaller ones of equal radius $r$ (highlighted orange).

Finally we have $2$ circles of the same radius $t$, which both touch the large (green) circles and the square.

How we can find a formula that calculates the radius $r$ of the $6$ small circles when inputting the radius $t$?

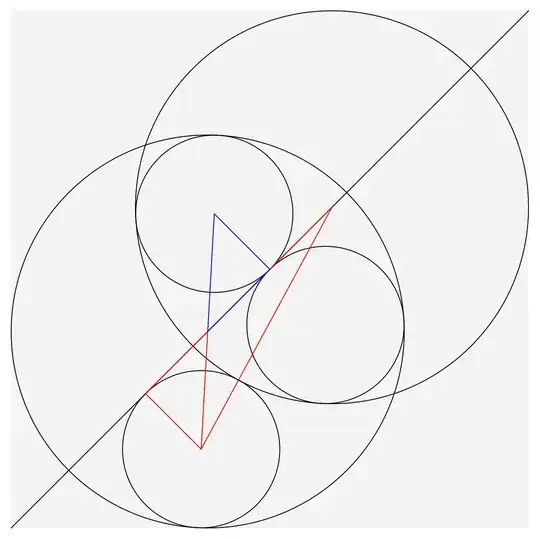
One idea to proceed might be to define a distance $d$ from the center of one of the large (green) circles to the point at which the large radius $R$ is touching one of the small (orange) circles. Then at least we would get the Pythagorean triangle equation $r^2+d^2=(R − r)^2$ as a possibly useful starting point:

Answer 1

Using your detail and variable names, I get this:

$\sqrt{(R+r)^2 - r^2} = 3d$

$\sqrt{(R+r)^2 - r^2} = 3\sqrt{(R-r)^2 - r^2}$

From there, you should reach $R = \frac{5}{2}r$.

With a little more work, the square width is $(5+\frac{\sqrt{10}}{2})r$.

Now this construction is for point $C$, the center of one of the circles having radius $t$:

The red construction circle, $B$, has radius $R$, same as the green circles. And we have this proportion:

$\frac{AC}{AB}=\frac{AE}{AD}$

I never did actually reach the end of the calculation, but it is all there. One thing to watch out for is that none of those orange circles touch the square. Four of them come quite near, but don't be fooled.

Answer 2

The blue triangle is easy and has already been illustrated by the OP. Without loss of generality, suppose the square is the unit square in the coordinate plane. Then the common point of tangency of the two small circles is $(1/2,1/2)$, and the distance between this point and a center of the larger circle is simply $d_1 = \sqrt{2}(1/2 - R)^2$. Therefore, the blue triangle corresponds to the equation $$2 (1/2 - R)^2 + r^2 = (R - r)^2.$$

Now let $d_2$ be the distance from $(1/2,1/2)$ to the point of tangency of the small circle that is outside one of the larger circles, with the diagonal line. Then we must have the simultaneous conditions $$(d_2 + d_1)^2 + r^2 = (R + r)^2, \\ (d_2 - d_1)^2 + r^2 = (R - r)^2.$$ The solution to this system is left as an exercise for the reader; we have $$\begin{align} r &= \frac{10 - \sqrt{10}}{45}, \\ R &= \frac{10 - \sqrt{10}}{18}, \\ d_1 &= \frac{\sqrt{10} - 1}{9\sqrt{2}}, \\ d_2 &= \frac{2 \sqrt{5} - \sqrt{2}}{9}. \end{align}$$

Note this uniquely fixes all of the circles in the square. This means the two externally tangent circles with radius $t$ are also uniquely determined, and their common radius is easily shown to obey the relationship $$(1-R-t)^2 + (R-t)^2 = (R+t)^2,$$ or $$t = 1 - 2 \sqrt{R} + R = \frac{28 - \sqrt{10} - 6\sqrt{20 - 2 \sqrt{10}}}{18}.$$

Answer 3

Let the centres of the green circles be $O_1$ (lower) and $O_2$ (upper).

Let $P$ be the midpoint of $O_1O_2$ which is also the centre of the square.

Let the uppermost two orange circles above the line $O_1O_2$ have centres $C_1$ (lower) and $C_2$ (upper).

Let $Q$ be the point where the circle centre $C_2$ touches the line $O_1O_2$.

Now if we write $O_1P=d$, then $O_2P=d$, and since $\triangle O_1C_1P\equiv\triangle O_2C_2Q$, then $O_2Q=d\implies O_1Q=3d$.

Applying Pythagoras to $\triangle O_1C_1P\implies (R-r)^2=d^2+r^2\implies d^2=R^2-2Rr$

Applying Pythagoras to $\triangle O_1C_2Q\implies (R+r)^2=9d^2+r^2\implies 9d^2=R^2+2Rr$

Solving these gives $$8R^2=20Rr\implies R=\frac{5r}{2}$$

From this we can get $$d=\frac15R^2\implies d=\frac{R}{\sqrt{5}}\implies d=\frac{r\sqrt{5}}{2}$$

Now let $B$ be the centre of the lower blue circle of radius $t$, and let $BP=y$.

Applying Pythagoras in $\triangle PC_1B\implies (R+t)^2=d^2+y^2$ $$\implies(R+t)^2-\frac{R^2}{5}=y^2$$ $$\implies \frac45R^2+2Rt+t^2=y^2$$

Hence, $$y^2=5r^2+5rt+t^2$$

Now consider the lengths of the diagonals of the square: we have $$2(y+t\sqrt{2})=2d+2R\sqrt{2}$$ $$\implies y+t\sqrt{2}=d+\frac52r\sqrt{2}=r\left(\frac{\sqrt{5}+5\sqrt{2}}{2}\right)$$

Substituting for $y$ we now have $$5r^2+5rt+t^2=\left[r\left(\frac{\sqrt{5}+5\sqrt{2}}{2}\right)-t\sqrt{2}\right]^2$$

So for a given value of $t$ you can obtain $r$ by solving a quadratic equation:

$$r^2\left(\frac{35+10\sqrt{10}}{4}\right)-rt(15+\sqrt{10})+t^2=0$$