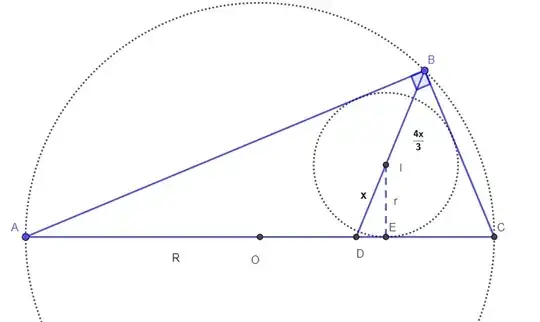
For reference: In a right angle triangle ABC, an interior bisector BD is traced, where I is or incenter, $\measuredangle B = 90 ^ o$ and $3BI = 4ID$. Find the relationship between the circumraio and inraio lenght of $\triangle ABC$. (Answer:3)
My progress: I made the drawing Inradius = r Circumradius = R
$r=\frac{a+c-b}{2}=\frac{ab}{a+b+c}\\ R = \frac{b}{2}\\ \frac{R}{r} = \frac{b}{a+c-b}$