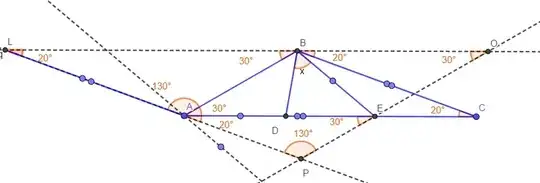
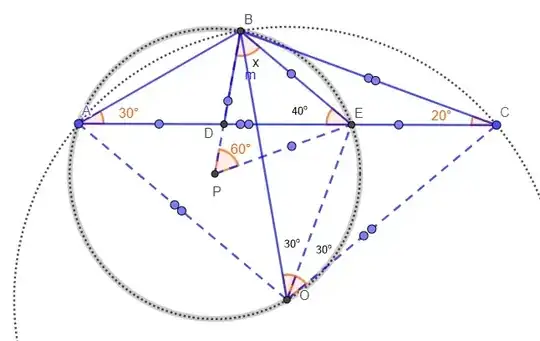
For reference: Calculate $x~ if AE = BC, and AD = BE$
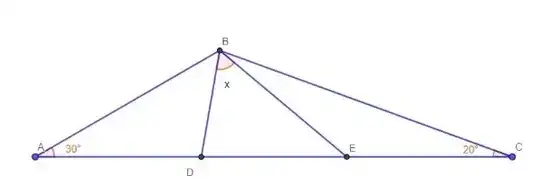
My progress: I tried for auxiliary lines...parallel to BC by A and parallel to BE by A... forming the parallelograms...I completed the Angles but I was unsuccessful...but I believe the solution is in the auxiliary lines