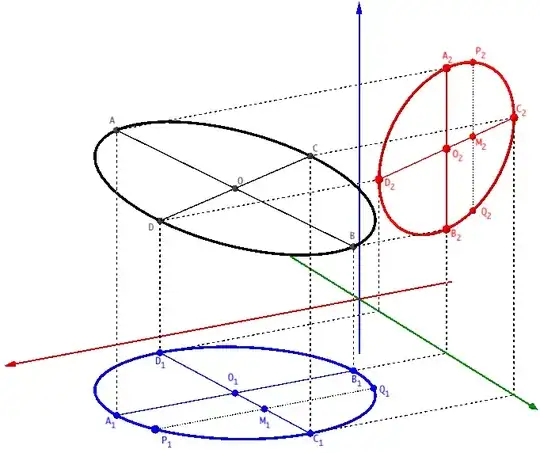
The projection onto the $xy$ plane (parallel to the $z$ axis) of the original ellipse defines an elliptical cylinder whose axis is parallel to the $z$ axis. And similarly the projection onto the $yz$ plane (parallel to the $x$ axis) of the original ellipse defines an elliptical cylinder whose axis is parallel to the $x$ axis. The equations of the these cylinders are, respectively,
$ (r-r_0)^T Q_1 (r-r_0) = 1 $ and $ (r-r_0)^T Q_2 (r-r_0) = 1 $, where
where $r = [x, y, z]^T$, and $r_0$ is the center of the original ellipse which can be found directly from the centers of of the two projections, and,
$Q_1 = \begin{bmatrix} R_1 D_1 R_1^T && 0_{2 \times 1} \\ 0_{1 \times 2} && 0 \end{bmatrix} $
$Q_2 = \begin{bmatrix} 0 && 0_{1 \times 2} \\0_{2 \times 1} && R_2 D_2 R_2^T \end{bmatrix} $
where $D_1, D_2$ are $2 \times 2$ diagonal matrices containing the reciprocal of the squares of the semi-axes lengths of the projected ellipses, and $R_1$ is a $2 \times 2$ rotation matrices with respect to the $x, y$ axes and $ R_2$ is a $2 \times 2$ rotation matrix with respect to the $y$ and $z$ axes.
Now we simply subtract the two equations, this leads to,
$ (r - r_0)^T (Q_1 - Q_2) (r - r_0) = 0$
Since we know that there are non-trivial solutions to this equation, then $\text{rank} (Q_1 - Q_2) $ must be $2$ (see remark below).
Thus, we can diagonalize $(Q_1 - Q_2)$ into
$Q_1 - Q_2 = R D R^T $
where one of the diagonal elements of $D$ is zero, one is positive, and one is negative. Define $p = R^T (r - r_0)$ then
$ p^T D p = 0 $
Assume that $D_{33} = 0$, and $D_{11} =\alpha \gt 0$ and $D_{22} = - \beta \lt 0 $, then
$ \alpha {p_1}^2 - \beta {p_2}^2 = 0 $
Hence, the vector $p$ can parameterized as
$p = t (1, \pm \sqrt{\dfrac{\alpha}{\beta} } , 0 ) + s (0, 0, 1) = t v_1 + s v_2 $
Hence $p$ lies in a plane spanned by $v_1, v_2$. (Actually, from the above expression, it is evident that there are two such planes).
Back to the expression for $r$, we have
$r = r_0 + R p = r_0 + t R v_1 + s R v_2 = r_0 + t w_1 + s w_2 $
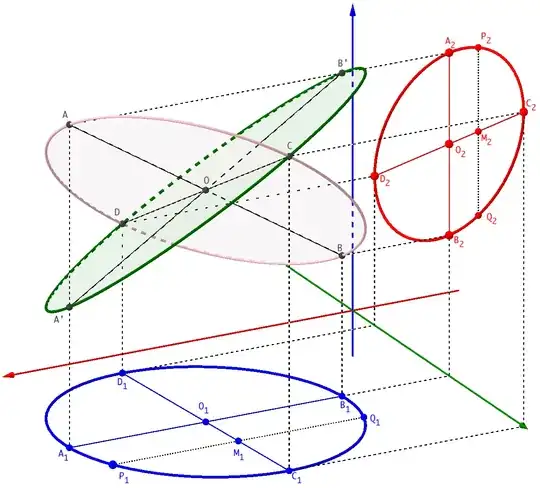
Hence, all we have to do now is intersect this plane spanned by $w_1 , w_2$ with the cylinder $ (r - r_0)^T Q_1 (r - r_0) = 1$.
Before we do that, we need to create two mutually orthogonal unit vectors $u_1, u_2$ that span the plane. Noting that $w_1$ is perpendicular to $w_2$, we only to have normalize $w_1, w_2$. Thus let $u_1 = w_1 /\| w_1 \|$ and $u_2 = w_2 /\|w_2 \| $,
Define the $3 \times 2 $ matrix $W = [u_1, u_2]$ , and the $2 \times 1$ vector $ u = [ t' , s' ]^T $
Then $ r = r_0 + W u $
Plug this into $(r - r_0)^T Q_1 (r - r_0) = 1 $ you end up with $u^T W^T Q_1 W u = 1$
One last step, diagonalize the $2 \times 2$ matrix $(W^T Q_1 W)$ into $R_w D_w R_w^T$, then the eigenvalues $(W^T Q_1 W)$ which are the diagonal elements of $D_w$
are simply the reciprocals of the semi-major and semi-minor axes lengths of the original ellipse. And the direction of the axes can be found using the rotation matrix $R_w$, this is because
$ u^T W^T Q_1 W u = u^T R_w D_w R_w^T u = v^T D_w v = 1 $ , where $ v = R_w^T u $
And we thus have $r = r_0 + V u = r_0 + V R_w v $
Thus the direction of the axes is given by the columns of the $3 \times 2$ matrix $V R_w$
We can even parameterize the original ellipse by solving $v^T D_w v = 1$ to be
$v = [ a \cos \theta , b \sin \theta ] $ , where $a \gt b$
It is assumed that $D_{w{11}} \lt D_{w{22}} $
Then,
$r = r_0 + (V R_w) [a \cos \theta, b \sin \theta ]^T $
Remark:
$\text{rank}(Q_1-Q_2)$ can also be $1$ in the special case where the plane of the original ellipse is perpendicular to the $xy$ plane or the $yz$ plane, resulting in a projection that is a straight line segment and not an ellipse in the normal sense. In this case, the plane of the original ellipse can be determined from the line segment, in the $xy$ plane and $z$ axis, or the line segment in the $yz$ plane and the $x$ axis, , and the solution method described above still applies.
Note that if the rank of $(Q_1 - Q_2)$ is $1$ then we will have $D_{11} \ne 0$ while $D_{22} = D_{33} = 0$ In this case, the plane in which vector $p$ lies is spanned by $(0, 1, 0)$ and $(0, 0, 1)$. The rest of the procedure detailed above remains the same.