0

For discrete random variable:
$$E(X)=\sum_{k=1}^{\infty}P(X\ge k)=\sum_{k=0}^{\infty}P(X>k)$$I have intuition of where it comes from since:
$P(X= 1)$.
$P(X= 2) + P(X= 2)$.
$P(X= 3) + P(X= 3) + P(X= 3)$.
...
If we sum them "Vertically", then we would see that it is the same as the above formula.

For continuous random variable:
We were presented with the following formula:
$$E(X)=\int_0^{\infty}(1-F_X(x))dx-\int_{-\infty}^0F_X(x)dx$$ I understand that it was presented to us this way, so we could use the first part if we know that $X$ is a positive random variable, but I couldn't quite get the idea behind the formula itself, The first integral looks like the one with the discrete random variable, since $1-F_X(x)=P(X>x)$, why we need to minus the second integral? why we didn't do it in the discrete formula?

Thanks in advance for any help!

Pwaol
  • 2,113

1 Answers1

2

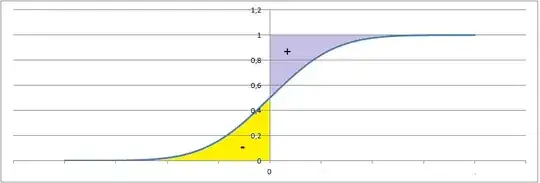
As per the continous formula you corrected posted this is the geometrical explanation

enter image description here

The expectation is the purple area minus the yellow one.

To verify this, simply integrate by parts you expression finding that

$$\int_0^{\infty}\left[1-F_X(x)\right]dx-\int_{-\infty}^0F_X(x)dx=\int_{-\infty}^{\infty}x f_X(x)dx=\mathbb{E}[X]$$

Similar reasoning can be applied to a discrete r.v.

integration by parts

$$I_1=\int_0^{\infty}\left[1-F_X(x)\right]dx=\underbrace{\left.x(1-F_X) \right]_{0}^{-\infty}}_{=0}+\int_0^{\infty}xf_X(x)dx$$

$$I_2=-\int_{-\infty}^0F_X(x)dx=-\left[\underbrace{\left.xF_X \right]_{-\infty}^{0}}_{=0}-\int_{-\infty}^{0}xf_X(x)dx\right]=\int_{-\infty}^0 xf_X(x)dx$$

tommik
  • 32,733
  • 4
  • 15
  • 34
  • Thanks alot! The second integral will always be negative so we subtract it in order to "add" them up? If you could please do another step or two about integrating by parts as I'm not sure what to do there exactly. – Pwaol Sep 21 '21 at 07:55
  • 1
    @Pwaol : added some details about the integration – tommik Sep 21 '21 at 08:03
  • Thanks for the help! all clear now, just my previous question, we subtract in order for us to add the negative area? (as in the image if the purple area was added to the negative yellow area we would get $0$?) – Pwaol Sep 21 '21 at 08:16
  • 1
    @Pwaol : no, the yellow area must be subtracted! In the picture I showed I took a CDF of a Standard Gaussian, thus actually $E(X)=0$ – tommik Sep 21 '21 at 08:19
  • I see, I was confused because I was introducted to it by these integrals: $E^+(X)=\int_0^{\infty}xf_X(x)dx$ and $E^-(X)=-\int_{-\infty}^0xf_X(x)dx$, and thus $E(X)=E^+(X)-E^-(X)$, so the minus in the definition of $E^-(X)$ is to make sure we are subtracting them? I could have did $E^-(X)=\int_{-\infty}^0xf_X(x)dx$ and then $E(X)=E^+(X)+E^-(X)$? – Pwaol Sep 21 '21 at 08:24
  • This also reveals a special case for non-negative random variables: the integral of the complementary CDF equals the expectation. See also: https://math.stackexchange.com/questions/64186/intuition-behind-using-complementary-cdf-to-compute-expectation-for-nonnegative – Peter O. Sep 21 '21 at 15:08