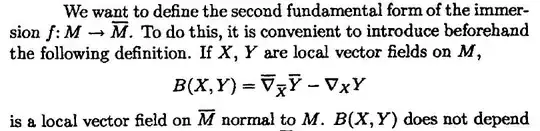1

I don't know why red line is right. In my view, since $$ S_\eta : T_pM\rightarrow T_pM $$ I think the diagonalize means that the matrix of $S_\eta$ is diagonal. Athough, I know that $S_\eta$ is linear about $\eta$, namely $$ S_{\eta+\delta}= S_\eta + S_\delta,~~~S_{k\eta} =kS_\eta $$ but why $[S_\eta, S_\delta]=0 $ equal to the red line ?

enter image description here

enter image description here

enter image description here

Enhao Lan
  • 5,829

1 Answers1

2

Each $S_\eta$ is a self-adjoint operator $T_pM \to T_pM$, so each $S_\eta$ is diagonalizable by the spectral theorem. Moreover $[S_\eta,S_\zeta]=0$ means that $S_\eta$ and $S_\zeta$ commute. It's a general linear algebra fact that a finite-dimensional family of commuting diagonalizable linear transformations are simultaneously diagonalizable.

Max
  • 3,937
  • Thanks, about the general linear algebra fact, which book I should read ? – Enhao Lan Sep 13 '21 at 00:57
  • 1
    You don't need a book for this if you already know about eigenspaces. Try proving it yourself (start with a pair of commuting diagonalizable transformations). This questions has also been answered on this website, e.g. https://math.stackexchange.com/questions/236212/prove-that-simultaneously-diagonalizable-matrices-commute – Max Sep 13 '21 at 07:42