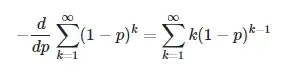I found this equality as a part of this proof and I am wondering how to get it using the chain rule as suggested by the author of the linked answer. I haven't touched calculus in a fair bit and thus I am rusty.
Chain rule:$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$
Since the series $\displaystyle\sum_{k=1}^\infty k(1-p)^{k-1}$ converges uniformly on $(0,1]$ and since\begin{align}\frac{\mathrm d}{\mathrm dp}(1-p)^k&=k(1-p)^{k-1}\times(-1)\text{ (by the chain rule)}\\&=-k(1-p)^{k-1},\end{align}you have\begin{align}-\frac{\mathrm d}{\mathrm dp}\sum_{k=1}^\infty(1-p)^k&=\sum_{k=1}^\infty\frac{\mathrm d}{\mathrm dp}-(1-p)^k\\&=\sum_{k=1}^\infty k(1-p)^{k-1}.\end{align}