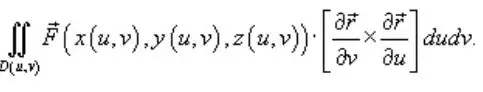In the formula for calculating surface integrals of second kind, we have:
But, this integral is denoted by $\int \int _S \vec{F}\cdot \hat{n}dS $ . So, should we always normalize the expression $ \frac{\partial \vec r }{\partial v} \times \frac{\partial \vec r}{\partial u} $ before substituting it into the formula?
Thanks in advance !
Here's a little derivation of the formula - hopefully it'll help you to answer your own question.
The definition of the surface integral tells us that $$ \iint_S \vec F \cdot d\vec S = \iint_S \vec F \cdot \hat n \, dS $$ where $\hat n$ is the unit normal vector to the surface. This equivalence is well described in chapter 16 of Stewart's book. Moving on, we know that $$ \vec r_u \times \vec r_v $$ is a vector normal to the surface parametrized as $\vec r(u,v)$. This vector must to normal to the surface because $\vec r_u$ and $\vec r_v$ are both curves tangent to the surface and their cross product gives a vector that perpendicular to each of them. To make this a unit vector, we simply divide it by it's length $\left| \vec r_u \times \vec r_v \right|$ and obtain $$ \hat n = \frac{\vec r_u \times \vec r_v}{\left| \vec r_u \times \vec r_v \right|} $$ Substituting this into the above integral, we obtain $$ \iint_S \vec F \cdot \left( \frac{\vec r_u \times \vec r_v}{\left| \vec r_u \times \vec r_v \right|} \right) \, dS $$ Furthermore, we know that $\left| \vec r_u \times \vec r_v \right|\, dA$ is the infinitesimal surface area element $dS$ (this is also well described in Stewart). Plugging this in, we get $$ \iint_D \vec F \cdot \left( \frac{\vec r_u \times \vec r_v}{\left| \vec r_u \times \vec r_v \right|} \right) \, \left| \vec r_u \times \vec r_v \right| \, dA $$ where $D$ is the domain of the parameters $u$ and $v$. This simplifies to $$ \iint_D \vec F \cdot \left( \vec r_u \times \vec r_v \right) \, dA $$ Any of these expressions can be used in computing the surface integral. However, using any of them before the final one would just be a recalcitrant implementation of the final formula as they would simplify to the same thing. If you're trying to compute the surface integral over $D$, the parameters of $u$ and $v$, then no, you do not need to scale the normal vector to length one.
Hope this helps!
