Once you take out the erroneous absolute value signs, $$\int \frac{\text{d} x}{2x^2-2x+1}=\frac{i}{2}\cdot\ln\left(\frac{2x-1+i}{2x-1-i}\right)+C$$
is a perfectly correct answer, and is in fact the same answer as $\arctan(2x-1)+C$ from the video.
First, the absolute value bars. As to what went wrong there, I think it's probably useful to think about why we need them in the case of $\int \frac{\text{d}x}{x}=\ln\lvert x\rvert+C$. I can't do better than the answers already posted to The Absolute Value in the Integral of $1/x$, but to provide a quick gloss: the natural logarithm is undefined outside of positive numbers, but $1/x$ is defined everywhere but $x=0$. Writing the anti-derivative as $\ln\lvert x\rvert+C$ let's us talk about the results of integrating $1/x$ both for $x>0$ and $x<0$. The need to prevent taking the natural logarithm of negative numbers doesn't come up here, so the absolute value bars only confuse.
The rest of this answer shows the equivalence of what you found with $\arctan(2x-1)+C$. The way in the video A quick warning. If you've already taken a course in complex analysis, these next few paragraphs are about to be a lot of words telling you things you already know, in which case you may want to skim rather than read, or even just try to work out how your answer is equivalent to the video's by yourself. I'm going to assume a good deal less background knowledge than that: namely, I'm going to write as if
- you've seen the complex plane before (but have not necessarily heard of the modulus and argument of a complex number)
- have heard of Euler's formula: $e^{i\theta}=cos\theta+i\sin\theta$,
- that you've previously worked with polar coördinates $(r,\theta)$,
- and otherwise this is all new to you.
That brings us to where you left off in your work, with the answer:
$$\frac{i}2\cdot[\ln(2x−1+i)−\ln(2x−1−i)]\text.$$ We can simplify this further by evaluating $\ln(2x-1+i)$ and $\ln(2x-1-i)$. To do that, though, we're going to need to have an idea what the natural logarithm of a complex number should be. Here is our agenda: 1) look at ways to express a complex number, 2) look at $e^z$ geometrically 3) define $ln(z)$ as the reverse of $e^z$ and 4) use the definition to compute $\ln(2x-1+i)$ and $\ln(2x-1-i)$ do a bit of algebraic clean-up to show the equivalence of the two answers.
Two views of the complex plane
Like with the Cartesian plane, we can refer to a complex number by either a "rectangular" or polar coordinate system. In rectangular coordinates, we write out the real and imaginary parts directly, for example: $z=3+i$. In polar coordinates we write out the modulus and the argument. The modulus is written $\lvert z\rvert$ and expresses the distance of the number from $0$ (in the case of $z=3+i$ this is $\sqrt{3^2+1^2}=\sqrt{10}$). The argument is the angle between the positive half of the real axis and the line connecting $0$ and $z$. In our example, Arg$(3+i)=\arctan(1/3)$. When we're thinking in terms of moduli and arguments, we tend to write complex numbers as $z=\lvert z\rvert e^{i\text{Arg}(z)}$. A picture of our running example shows $z=3+i=\sqrt{10}e^{i\arctan(1/3)}$ below.
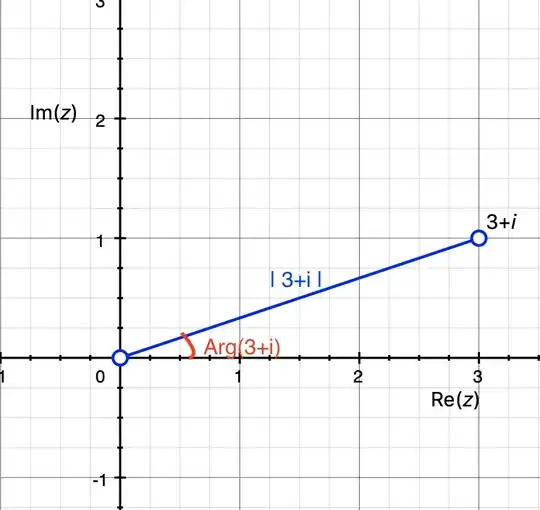$3+i$, it lies $3$ units out on the real axis and one unit up on the imaginary axis. It also has a modulus of length $|3+i|=\sqrt{10}$ indicated by the blue line, and an argument of $\arctan(1/3)$ drawn in red." />
A Geometric look at $e^z$
More than anything we want $\ln(z)$ to be the inverse of $e^z$, so looking at $e^z$ is a good starting point.
If we know $e^x$ for real-valued $x$, what should $e^z$ be? Start with a complex number $z=x+iy$ and apply the usual rules of exponents: $e^{x+iy}=e^x\cdot e^{iy}\text.$ Looking a little closer, we can also recognize this as a representation of a complex number using its argument and modulus. We have $\lvert e^z\rvert = e^x$ and $\text{Arg}(e^z)=y$, give or take an integer multiple of $2\pi$. In other words, $e^z$ bridges the rectangular and polar representations of the complex plane by taking a number $z$, letting the real part of $z$ determine the modulus of $e^z$, while the imaginary part of $z$ determines the argument of $e^z$.
One thing to notice is that, unlike on $\mathbb{R}$, here $e^z$ is not injective. Even though $5+i\pi\neq 5+3i\pi$, we have $e^{5+i\pi}=e^{5+3i\pi}$. This is why we had to add the caveat of "give or take an integer multiple of $2\pi$" earlier. When we ask about the angle between the real axis and the line from $0$ to $1+i$, there's some ambiguity. Do we mean $\pi/4$? Do we mean $9\pi/4$? Either is a valid choice, but in order to make $\text{Arg}(z)$ a well-defined function, we need to remove that ambiguity. Usually, we do this by saying $\text{Arg}(z)$ has the range $(-\pi,pi]$. Occasionally we'll specify that $\text{Arg}(z)$ falls in a different range, like $(0,2\pi]$. Anyway, whatever range we specify, what we're doing is removing "duplicate" angles so that $\text{Arg}(z)$ has a clear value.
Natural logarithms of complex numbers
In principle, what we want out of the function $\ln(z)$ is to have $\ln(e^z)=z$. For the reasons just explained, we can't quite get there, but our motivating logic for defining $\ln(z)$ is still to work in reverse of $e^z$. If $f(z)=e^z$ turns the real part of $z$ into the modulus of $e^z$, we'll want $f^{-1}(z)=ln(z)$ to turn the modulus of $z$ into the real part of $\ln(z)$. If $f(z)=e^z$ turns $z$'s imaginary part into the argument of $e^z$, we'll want $f^{-1}(z)=\ln(z)$ to turn the argument of $z$ into the imaginary part of $\ln(z)$. Putting this all together for a complex number with modulus $r$ and argument $\theta$, we say $$\ln(re^{i\theta})=\ln(r)+i\theta\text,$$ with the right-hand $\ln(r)$ the natural logarithm we already know over the real numbers. I'm also assuming $r$ is positive (if it is negative, we may make it positive and adjust the argument of $z$ by $\pi$). Incidentally, this version natural logarithm can handle negative numbers. If $x<0$, then $\ln(x)=\ln\lvert x\rvert+i\pi$. The natural log of $0$ remains undefined.
Computing $\ln(2x-1\pm i)$
Now let's get to evaluating. We have $2x-1\pm i$. Life will be easier if we have these numbers as moduli and arguments. We calculate $$\lvert 2x-1\pm i\rvert=\sqrt{(2x-1)^2+(\pm 1)^2}=\sqrt{4x^2-4x+2}\text.$$ As for arguments, we have that $\text{Arg}(2x-1+i)=\arctan(1/(2x-1))$ and $\text{Arg}(2x-1-i)=\arctan(-1/(2x-1))$. If we take the values of $\text{Arg}(z)$ to run between $-\pi$ and $\pi$, this means we can write $\text{Arg}(2x-1+i)=-\text{Arg}(2x-1-i)$. Now we have:
$$\begin{align}\ln(2x-1+i)&=\left(\sqrt{4x^2-4x+2}+i\arctan\left(\frac{1}{2x-1}\right)\right)\text{, and}\\
\ln(2x-1-i)&=\left(\sqrt{4x^2-4x+2}-i\arctan\left(\frac{1}{2x-1}\right)\right)\text{.}\end{align}$$
So, $$\begin{align}\frac{i}{2}\left(\ln(2x-1+i)-\ln(2x-1-i)\right)&=\frac{i}{2}\left(2i\arctan\left(\frac{1}{2x-1}\right)\right)\\&=-\arctan\left(\frac{1}{2x-1}\right)\\&=-\frac{\pi}{2}+\arctan\left({2x-1}\right)\text,\end{align}$$
with the last line using the fact that $\arctan(a/b)+\arctan(b/a)=\pi/2$.
Finally, we add a constant of integration and fold the $-\pi/2$ into it:
$$\int \frac{\text{d} x}{2x^2-2x+1}=\arctan\left({2x-1}\right)+C\text.$$
$3+i$, it lies 
