Consider the ball $B$ in $\mathbb{R}^3$ of radius $2\pi$, centered on the origin.
Any point $u\in B$ represents a rotation through an angle $|u|$ radians about the directed axis represented by $u$. Note there is no ambiguity with $0\in B$ as a rotation through $0$ radians is the identity map - e.g. we do not need an axis.
Note also that all rotations through $2\pi$ radians are the same regardless of axis, so we may quotient the boundary of $B$ to a point, to obtain a sphere $S^3$ and still have every element of $S^3$ representing a well defined rotation.
Any rotation in $SO(3)$ will be represented by precisely two points in $S^3$: a non-trivial rotation will be $\theta$ radians clockwise about some directed axis represented by a unit vector $u$, with $\theta\in [0,2\pi]$, so will be represented by $\theta u\in S^3$. However it will also be represented by $-(2\pi-\theta)u\in S^3$.
Thus $SO(3)\cong S^3/(\mathbb{Z}/2)$ in a visual way - a rotation is represented by a point in $S^3$, where the distance from the identity is the angle of rotation, and direction from identity is axis of rotation.
An easy way to see the natural fibration $SO(3)\to S^2$ is to define it as as evaluation on a point of $S^2$. That is fix a point $x\in S^2$ and map a rotation $A\in SO(3)$ to $Ax\in S^2$.
Finally, to visualise the non-trivial element in $\pi_1(SO(3))$ simply pick an axis and rotate about it going form $0$ radians to $2\pi$ radians. This lifts to a path in $S^3$ going from the origin to the point representing rotations by $2\pi$ radians. Thus it represents a non-trivial element of $\pi_1(SO(3))$ (to be trivial it would have to lift to a loop).
Let $f:S^3\to SO(3)\to S^2$ denote the composition of the quotient map $S^3\to SO(3)$ and the fibration described above, sending each $A\in SO(3)$ to $Ax$.
The fiber $F_y$ in $SO(3)$ above a point $y\in S^2$ is the set of rotations which map to $y$. That is $F_y$ is the set of rotations $\{C| Cx=y\}$.
If $Ax=y$ then $F_y=\{AT_\theta |\theta\in[0,2\pi]\}$, where $T_\theta$ denotes a rotation through $\theta$ radians about $x$.
Consider in particular $f^{-1}(x)$. This is all points in $S^3$ which map to a $T_\theta$. That is precisely the line through the origin and $x$. Note this line is actually a circle, as the boundary points of $B$ are identified. In other words $2\pi x=-2\pi x$ in $S^3$.
Now consider the fiber $F_y$ where $y$ is the point in $S^2$ opposite $x$. The fiber above $y$ in $SO(3)$ is all $\pi$ radian rotations about an axis perpendicular to $x$. These are precisely the rotations taking $x\mapsto y$.
Thus $f^{-1}(y)$ is the circle about the origin of radius $\pi$, perpendicular to $x$. Thus we can see that $f^{-1}(x)$ and $f^{-1}(y)$ form a pair of linked circles in $S^3$.
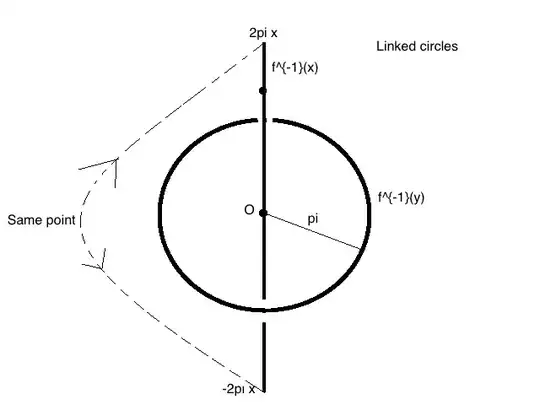
Note that for any points $z\neq w\in S^2$ there are paths in $S^2$ from $x$ to $z$ and from $y$ to $w$ which do not cross. Following these paths gives us isotropies of the fibers from $f^{-1}(x) \to f^{-1}(z)$ and $f^{-1}(y) \to f^{-1}(w)$, which also do not cross. Thus any pair of fibers $f^{-1}(z)$ and $f^{-1}(w)$ will be linked in the same way as in the picture above.
