$S=\displaystyle \lim\limits_{n \rightarrow \infty}(1/n^6+32/n^6+...1/n)$ and $T=...$ prove that $S+T>1/3$

Question

$S=\displaystyle \lim\limits_{n \rightarrow \infty}(1/n^6+32/n^6+...1/n)$ and $T=\displaystyle \lim\limits_{n\rightarrow \infty}(1/n^6+32/n^6+...(n-1)^5/n^6)$, then prove that $S\rightarrow \frac{1}{6}^+,$ $T\rightarrow \frac{1}{6}^-$ and $S+T>1/3 $

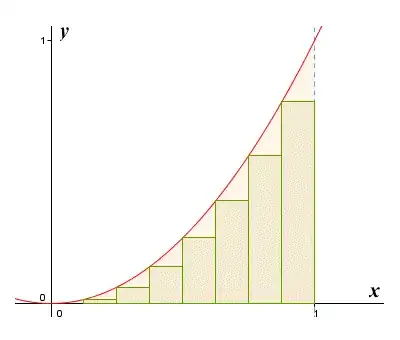
A definite integral shows the area under the curve for any function between two points which are called limits. We can integrate a function by dividing the area under the graph to small rectangles, decreasing the breadth of the rectangles to an infintesimally small quantity $dx$ and assuming there are an infinite number of rectangles.

$T=\int_0^1 x^5=1/6$ approximately. I think it will be a little less than $1/6$ because the last term is $(n-1)^5$. I can't understand why $S$ will be larger than $1/6$.

When we integrate using the rule $\int x^n=x^{n+1}/(n+1)+c$ , are we calculating the exact area under the graph or are we excluding the infinitesimally small areas left after filling the graph with an infinite number of rectangles. I.e are the areas shaded light pink in the graph accounted for or not.

Please help me with the question :)

Answer 1

$S > 1/6$ because the first rectangle starts at $1/n^6$ (instead of at $0$ as it does for $T$), so all the rectangles are above the curve, not below.

Therefore the sum of the rectangles is greater than the area.

As to why $S+T > 1/3$, I'd have to think about it. My first guess is because $f''(x) > 0$. But there might be a simple geometric reason.

---

In response to the comment.

If $f(x) \ge 0$, $f'(x) > 0$, and $a < b$ then $f(a) \lt \dfrac1{b-a}\int_a^b f(x) dx \lt f(b) $. This just says that the average value is between the minimum and maximum values.

Set $a = \dfrac{k-1}{n}$ and $b = \dfrac{k}{n}$ and sum.

Note that the inequality is reversed if $f'(x) < 0$.

Answer 2

Notice that the sums $T_n$ and $S_n$ appearing in the limits correspond to the lower and upper Darboux sums respectively, to the integral of the function $f(x)=x^5$ over the interval $[0,1]$ with respect to uniform partition $P_n=\{k/n:1\leq k\leq n\}$: $$T_n=\frac{1}{n}\sum^n_{k=1}\frac{(k-1)^5}{n^5}=L(f,P_n)< \int^1_0 x^5\,dx=\frac16 <S_n=U_n(f,P_n)=\frac1n \sum^n_{k=1}\frac{k^5}{n^5}$$

The trapezoidal approximation to the integral with respect to the uniform partition gives

$$ \tau(f;P_n)=\sum^n_{k=1}\frac{1}{n}\frac{\tfrac{k^5}{n^5}+\tfrac{(k-1)^5}{n^5}}{2}=\frac{1}{2}(T_n+S_n)$$ Since $f$ in convex, the line that joins the points $\big(\tfrac{k-1}{n},\frac{(k-1)^5}{n^5}\big)$ and $\big(\tfrac{k}{n},\frac{k^5}{n^5}\big)$ is above the graph of the function $f$ in the interval $I_k=\big[\tfrac{k-1}{n},\tfrac{k}{n}\big]$. Hence, the area of the trapezoid with vertices $\big(\tfrac{k-1}{n},0\big)$, $\big(\tfrac{k-1}n,\tfrac{(k-1)^5}{n^5}\big)$, $\big(\tfrac{k}{n},0\big)$, and $\big(\tfrac{k}n,\tfrac{k^5}{n^5}\big)$ is larger that the area between the graph of $f$ and the horizontal axis in the interval $\big[\tfrac{k-1}{n},\tfrac{k}{n}\big]$, that is $$\int^{k/n}_{(k-1)/n}x^5\,dx < \frac{(k-1)^5+k^5}{2n}$$ Consequently $$\frac16=\int^1_0x^5\,dx=\sum^n_{k=1}\int^{k/n}_{(k-1)/n}x^5\,dx<\sum^n_{k=1}\frac{k^5+(k-1)^5}{2n}=\frac{S_n+L_n}{2}$$