What is $\lim\limits_{n \to \infty}\sum\limits_{k=1}^n \frac{1}{k}$

Question

Possible Duplicate:
Why does 1/x diverge?

I'm a math tutor. This is a high school level problem. I'm unable to solve this.

What is the value of:

$\lim\limits_{n \to \infty}\sum\limits_{k=1}^n \frac{1}{k}$

Answer 1

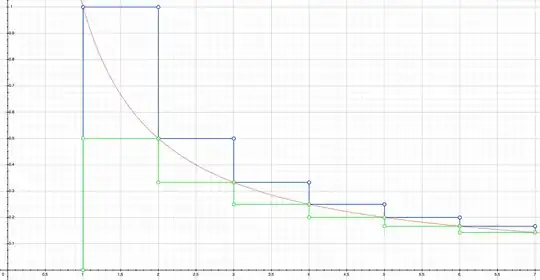
From the figure, you can see that the area under the blue-curve is bounded below by the area under the red-curve from $1$ to $\infty$.

The blue-curve takes the value $\frac1{k}$ over an interval $[k,k+1)$

The red-curve is given by $f(x) = \frac1{x}$ where $x \in [1,\infty)$

The green-curve takes the value $\frac1{k+1}$ over an interval $[k,k+1)$

The area under the blue-curve represents the sum $\displaystyle \sum_{k=1}^{n} \frac1{k}$ while the area under the red-curve is given by the integral $\displaystyle \int_{1}^{n+1} \frac{dx}{x}$ while the area under the blue-curve represents the sum $\displaystyle \sum_{k=1}^{n} \frac1{k+1}$

Hence, we get $\displaystyle \sum_{k=1}^{n} \frac1{k} > \displaystyle \int_{1}^{n+1} \frac{dx}{x} = \log(n+1)$

$\log(n+1)$ diverges as $n \rightarrow \infty$ and hence $$\lim_{n \rightarrow \infty} \displaystyle \sum_{k=1}^{n} \frac1{k} = + \infty$$

By a similar argument, by comparing the areas under the red curve and the green curve, we get $$\displaystyle \sum_{k=1}^{n} \frac1{k+1} < \displaystyle \int_{1}^{n+1} \frac{dx}{x} = \log(n+1)$$ and hence we can bound $\displaystyle \sum_{k=1}^{n} \frac1{k}$ from above by $1 + \log(n+1)$

Hence, $\forall n$, we have $$\log(n+1) < \displaystyle \sum_{k=1}^{n} \frac1{k} < 1 + \log(n+1)$$

Hence, we get $0 < \displaystyle \sum_{k=1}^{n} \frac1{k} - \log(n+1) < 1$, $\forall n$

Hence, if $a_n = \displaystyle \sum_{k=1}^{n} \frac1{k} - \log(n+1)$ we have that $a_n$ is a monotonically increasing sequence and is bounded.

Hence, $\displaystyle \lim_{n \rightarrow \infty} a_n$ exists. This limit is denoted by $\gamma$ and is called the Euler-Mascheroni constant.

It is not had to show that $\gamma \in (0.5,0.6)$ by looking at the difference in the area of these graphs and summing up the area of these approximate triangles.

Answer 2

You'd think it would converge but it doesn't.

An easy way to see this is to consider the subsequences from $\frac1{2^k}$ to $\frac1{2^{k+1}}$. Since $\frac1{2^{k+1}}$ is less than $\frac1{2^k}$, consider replacing all values between them with the last one. That is:

$$1 + 1/2+1/4 + 1/4+1/8 + 1/8 + 1/8+1/8+1/8+ 1/16 + 1/16+...$$

Since each subsequence sums to $1/2$, each time you go from $n = 2^m$ to $n=2^{m+1}$, you're adding 1/2, so in the limit it won't ever converge.

Answer 3

It diverges to infinity as $\log n$. You can see Wikipedia