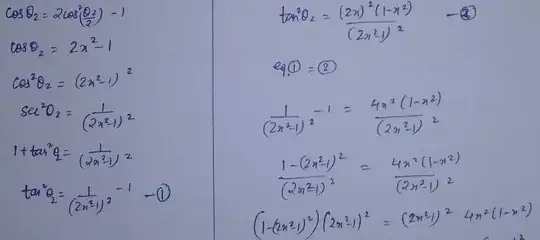Sometimes correct answer does not come while solving inverse trigonometric equations?

Question

I have a trigonometric equation in which we have to find the values of x. Here is the solution which i have done, but the answer is x ∈ (0,1). Why it is that sometimes when we solve inverse trigonometric equations , the answer does not match with the original answer and we have to always check by putting our values of x in the given equation to verify, even if we have done each and every step properly? please see this image:

It's a simple range issue. For negative $x$, the left hand side of the original equation is greater than $\pi$. The range of inverse cotangent only goes up to $\pi$ — Ninad Munshi, Aug 25 '21 at 05:37
For some basic information about writing mathematics at this site see, e.g., basic help on mathjax notation, mathjax tutorial and quick reference, main meta site math tutorial and equation editing how-to. — , Aug 25 '21 at 06:09

score 1 · Answer 1 · answered Aug 25 '21 at 16:15

$$2\arccos(x)=\mathrm{arccot}\left(\frac{2x^2-1}{2x\sqrt{1-x^2}}\right)$$

The immediate implicit restrictions:

$x\neq0$
$1-x^2>0,\;$ i.e., $\;x\in(-1,1)$
the left-side principal domain and principal range are $[-1,1]$ and $[0,2\pi],$ respectively.

So, $\,x\in(-1,0)\cup(0,1).$

So, $$-1<2x^2-1<1$$ and $$-2<2x\sqrt{1-x^2}<2;$$ so, $$\frac{2x^2-1}{2x\sqrt{1-x^2}}\in\mathbb R;$$ so, the right-side principal domain is $\mathbb R;$ so, the right-side principal range is $(0,\pi).$

So, the left-side effective (restricted) range is $(0,\pi);$ so the left-side effective (restricted) domain is $(0,1).$

Hence, the solution set must be a subset of $$(0,1).$$

Sometimes correct answer does not come while solving inverse trigonometric equations?

1 Answers1