Limits of composite functions where the function is discontinuous

Question

Limit of a composite function that isn't continuous: Take $$\lim_{x\to 0}f(g(x))$$ where $f$ is discontinuous at $0$. What should I do if I know the graphs of these functions and as I said $f$ is discontinuous at $0$ but the whole limit does exist?

My question rather is, how do I show the steps? Like I don't want to just directly put this equal to 0, but rather follow steps, how should I write the steps? because I can't write $\lim_{x\to 0}f(g(x))=f(\lim_{x\to 0}g(x))$ since $f$ isn't continuous at $0$.

Answer 1

We have that

$$\lim_{x\to 0}g(x)=2$$

and $f(x)$ has a removable discontinuity at $x=2$ therefore the limit exists with

$$\lim_{x\to 2}f(x)=0$$

and then we can conclude that

$$\lim_{x\to 0}f(g(x))=0$$

Note that continuity is not a necessary condition to determine the limit, what we need is that limits exist and that $g(x)\neq 2$ in a certain neighborhood of zero.

For related and detailed discussion on that point refer to:

• Finding a limit using change of variable- how come it works?
• Limit of the composition of two functions with f not necessarily being continuous.

Answer 2

Given real functions $f, g$, we can say $$\lim_{x \to a} f(g(x)) = f\left(\lim_{x \to a} g(x)\right) \tag{$\star$}$$ in the following circumstances:

• If $L = \lim_{x \to a} g(x)$ exists and $f$ is continuous at $L$, or
• If $L = \lim_{x \to a} g(x)$ exists, $g(x) \neq L$ for $x$ sufficiently close to $L$, and $\lim_{x \to L} f(x)$ exists.

The second case holds in the given question (note how $g(x) \neq 2$ for $x$ close to $0$), so we can still indeed use $(\star)$.

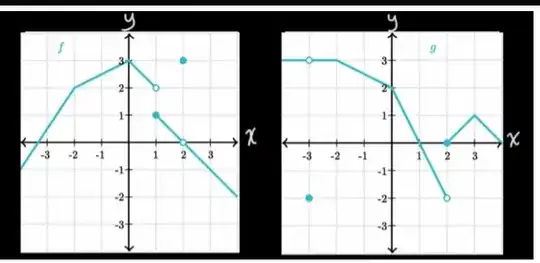
There are finer versions of this that may be helpful in certain circumstances. Consider the following limit given the above graphs: $$\lim_{x \to 3} f(g(x)).$$ Neither of the above conditions hold, since the limit $\lim_{x \to 1} f(x)$ does not exist. But, since $g(x) < 1$ for $x$ close to, but not equal to $3$, this tells us that $$\lim_{x \to 3} f(g(x)) = \lim_{x \to 1^-} f(x) = 2,$$ since $g(x)$ is producing function values close to but less than $1$, and we are substituting them into $f$.

I wouldn't look for a complete set of steps to solve problems like these. Try to build an intuition for what is going on.