1

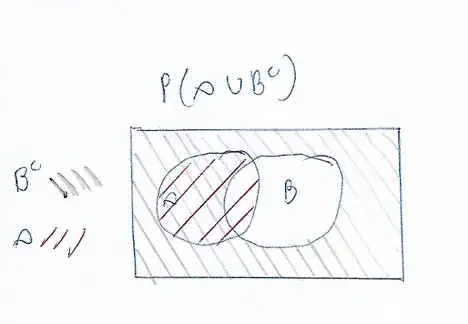
If A and B are independent events such that $Pr(A)=1/3$ and $Pr(B)>0$, what is the value of $Pr(A$ $\cup$ $B^c$$|B)=?$

From what I can understand , if we use the conditional probability formula , the numerator will be $Pr(A$ $\cup$ $B^c$ $\cap$ $B)$ which will be $0$ and therefore the answer is $0$ however im not sure. Can someone confirm or tell me where im going wrong?

Kanika Adhikari
  • 45
  • 1
    The set $A\cup B^c\cap B$ is not well defined. You mean to write $(A\cup B^c)\cap B$. Also, you should use the formula $$(A\cup B)\cap C=(A\cap C)\cup(B \cap C)$$ – user429040 Aug 21 '21 at 18:57

2 Answers2

2

$$P(A \cup B^c|B)\\=\frac{P(\left(A \cup B^c \right)\cap B)}{P(B)}\\=\frac{P(A\cap B)}{P(B)}\\=\frac{P(A)P(B)}{P(B)}\\=P(A)\\=\frac13$$

(The simplification at the second equality is obtained using either a Venn diagram or one of the distributive laws of set algebra.)

ryang
  • 38,879
  • 14
  • 81
  • 179
2

You can make a venn-diagramm.

enter image description here

If we now intersect this the marked area with $B$ then we obtain $A\cap B$.

Therefore $P((A\cup B^c)\cap B)=P(A\cap B)\stackrel{\textrm{ind.}}{=}P(A)\cdot P(B)$

callculus42
  • 30,550