This is a real-world problem I've got to deal with, so help appreciated. The diagram looks like this:
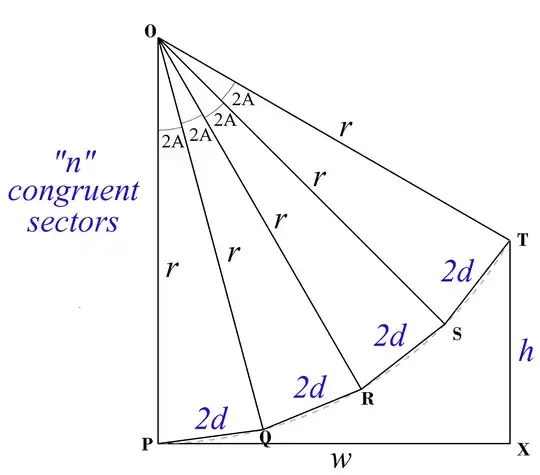The diagram shows 4 congruent sectors of a circle radius r, each of angle 2A, cut into triangles by chords length 2d at the circumference. The circle is shown in light grey, dotted. OPX and PXT are right angles, and POT < 90 degrees. The actual number of sectors n varies; n=4 is just an example. It may be assumed 3 <= n <= 6, and that n, d and h (all coloured blue) are given. A, r and w are unknown.
Problem: solve for r.
Bonus points: solve for r in a way that's easy to use within Excel (where this ultimately needs to end up).......
The problem I have, relates to the fact that the actual number of sectors n is itself a parameter. I can't think of a way to solve it generally, that doesn't require some pretty horrific trigonometric identity expansions, possibly leading to some pretty nasty equations to simplify in sin(A) or cos(A), and their sums and products. That's a problem as I plan to use it within Excel, as part of a larger calculation spreadsheet.
It's trivial to solve with iteration, or programmatically, but because of the apparent presence of varying terms in sin/cos A, sin/cos 2A, sin/cos 3A etc, it's unclear if there is an elegant solution. Of course one can break all of those down using sin/cos addition formulae, but when "n" is itself a variable that's going to get incredibly messy in a spreadsheet calculation. Another way would be to hard code formulae for each of the 6 possible values of "n" and choose appropriately using switch() or if() logic. That's pretty horrible too. Because I'd still have to reduce the sin/cos(A), sin/cos(2A) etc terms by expansion, and then manually solve all 6 resulting equations, before writing the individual solutions into Excel.
The symmetry seems to be crying out for a totally different approach than obtaining a formula for the distances from PX to each of Q, R, S then finally T, in terms of A, sin/cos A, sin/cos 2A, 3A, ..., then expanding all these, then solving formulaically...... and then finally, repeating that for each possible value of n. But I can't think what other way there is, if any.
At a pinch I'll gladly take an Excel VBA solution, if thats best, because I can't think how to avoid the expansion of trig identities, either. But perhaps I've missed a trick and there's an easier way? Even if not, perhaps there's more or less efficient ways to solve this, or it can be rewritten as a "well known" trigonometric series in sin(1x), sin (2x), ..., sin(nx), and perhaps some approach is amenable to simplifying enough to throw into Excel?
