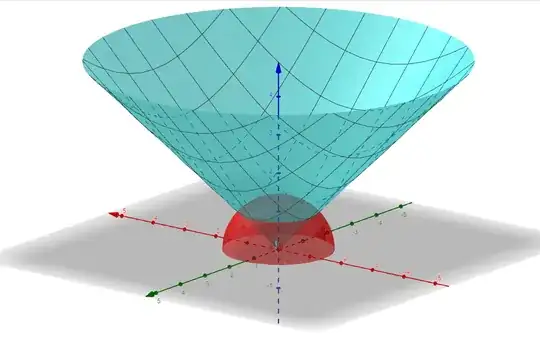
I have a domain for an integral given by: $$\sqrt{x^2+y^2} \le z \le \sqrt{2-x^2-y^2}$$
I've sketched the domain on a plane and can see the shape it makes (a sort of diamond shape) but in my question I'm asked to find the the two surfaces forming the boundary of this domain and I'm not entirely sure what this means/what this is. I can't really picture any boundaries.
I'll put an image of my plane and if anyone could explain/show what these boundaries are it would really help, thanks in advance.