Determine if $\sum^{\infty}_{n=1}\int^{\frac{\sin n}{n}}_0\frac{\sin x}{x} \, dx $ is converges or diverges.

Question

Could someone please show me how to do it? And especialy showing why $\lim_{n\to\infty}\int^{\frac{\sin n}{n}}_0\frac{\sin x}{x} \, dx=0$

(I know that $\lim_{n\to\infty} \frac{\sin n}{n}=0$)

score 4 · Accepted Answer · edited Apr 13 '17 at 12:21

4

This is edited version. Thanks to Tigran Saluev for pointing out the mistatke.

By his argument your series converges iff the series $$ \sum\limits_{n=1}^\infty\frac{|\sin n|}{n}\tag{1} $$ converges. Note that $$ \sum\limits_{n=1}^\infty\frac{|\sin n|}{n}\geq\sum\limits_{n=1}^\infty\frac{\sin^2 n}{n}=\frac{1}{2}\sum\limits_{n=1}^\infty\frac{1}{n}-\frac{1}{2}\sum\limits_{n=1}^\infty\frac{\cos 2n}{n} $$ The first term diverges as harmonic series diverges. The second term converges since $$ \sum\limits_{n=1}^\infty\frac{\cos 2n}{n} =\Re\left(\sum\limits_{n=1}^\infty\frac{e^{i\cdot 2n}}{n}\right) =\Re\left(\sum\limits_{n=1}^\infty\frac{z^n}{n}\biggl|_{z=e^{2i}}\right) =\Re\left(-\ln(1-z)|_{z=e^{2i}}\right)<\infty $$ Thus the series $(1)$ diverges, hence your series diverges too.

edited Apr 13 '17 at 12:21

Community

1

answered Jun 17 '13 at 08:19

Norbert

56,803

Norbert, thank you very much! – 17SI.34SA Jun 17 '13 at 08:22
@17SI.34SA see edits to my answer. Previous version was wrong – Norbert Jun 17 '13 at 10:46
This is a nice idea, but the power series of $\ln(1-z)$ has radius of convergence 1, so how do you know that the power series converges when $z=e^{2i}$? – Charles Roddie Dec 01 '19 at 23:44

Tigran Saluev · Answer 2 · 2013-06-17T09:23:54.087

$\frac{\sin x}{x}$ is a continuous function, thus $$\lim_{a\rightarrow 0}\int_0^a \frac{\sin x}{x}\,dx\ \ \ \mbox{ is always equal to } 0.$$ But that is not enough.

$\frac{\sin x}{x}$ is also positive in a neighborhood of 0, thus all the integrals for $n$ greater than some fixed $N$ are positive. It doesn't depend on the sign of $\frac{\sin n}{n}$, since the integrated function is even. But the fact $\frac{\sin n}{n}$ is not necessarily positive forbids you to write $$\int_0^{\frac{\sin n}{n}} \frac{\sin x}{x}\,dx \le \frac{\sin n}{n} $$ like Norbert has done. Correct estimate looks like $$\int_0^{\frac{\sin n}{n}} \frac{\sin x}{x}\,dx \le \frac{|\sin n|}{n}.$$ So the solution is not that simple.

$\frac{\sin x}{x}$ is decreasing and convex on $[0, 1]$:

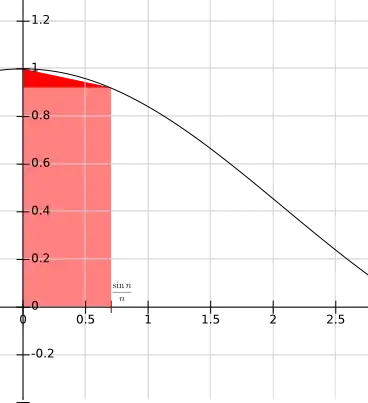
sin(x) / x decreasing and convex

So we can estimate the integral from below as the square of highlighted region: $$ \int_0^{\frac{\sin n}{n}} \frac{\sin x}{x}\,dx \ge \left.\frac{\sin x}{x}\right|_{x=\frac{|\sin n|}{n}}\cdot\frac{|\sin n|}{n} + \frac{1}{2}\cdot\frac{|\sin n|}{n}\cdot\left(1 - \left.\frac{\sin x}{x}\right|_{x = \frac{\sin n}{n}}\right) = $$ $$ = \frac{1}{2}\sin\left(\frac{|\sin n|}{n}\right) + \frac{1}{2}\frac{|\sin n|}{n}. $$ Thus, including my remark on Norbert's answer, your series converges if and only if $$\sum_{n=1}^{\infty}\frac{|\sin n|}{n}$$ converges.

For the first part, I would say that $ \frac{\sin x}{x} $ is a bounded function implies that the limit is zero. Continuity is neither necessary nor sufficient I think. For example, $ \frac{1}{x} $ is continuous on $ (0, \infty) $ but $ \lim\limits_{a \to 0} \int_0^a \frac{1}{x} \ dx \neq 0 $. — Jon Claus, Jun 19 '13 at 03:12
@JonClaus, you're totally right. But not any bounded function is integrable. We could say $\frac{\sin x}{x}$ is bounded and integrable thus the limit is zero. — Tigran Saluev, Jun 19 '13 at 12:42
The inequalities apply only when $\sin n$ is positive, and this condition is the condition for absolute convergence only. — Charles Roddie, Dec 02 '19 at 00:29

score 1 · Answer 3 · answered Dec 02 '19 at 00:28

Let $I_n=\int_{0}^{\frac{\sin n}{n}}{\frac{\sin x}{x}}dx$.

$I_n$ is between $a_n=\int_{0}^{\frac{\sin n}{n}}{\frac{x}{x}}dx=\frac{\sin n}{n}$ and $\int_{0}^{\frac{\sin n}{n}}{\frac{x-\frac{x^3}{6}}{x}}dx=\frac{\sin n}{n}-\frac{\left(\sin n\right)^3}{18n^3}$, and the difference $|I_n-a_n|\le\frac{\left|\sin n\right|^3}{18n^3}\le \frac{1}{n^3}$, whose sum converges absolutely.

So $\sum_{0}^{\infty}{I_n}$ converges (absolutely) if and only if $\sum_{0}^{\infty}{a_n}=\sum_{0}^{\infty}{\frac{\sin n}{n}}$ converges (absolutely).

And $\sum_{0}^{\infty}{\frac{\sin n}{n}}$ converges (Does $\sum\frac{\sin n}{n}$ converge?), but not absolutely.

score 1 · Answer 4 · answered Jun 17 '13 at 08:17

Hint for the second part of your question: The mean-value theorem shows that $\int_0^{\frac{\sin{n}}{n}} \frac{\sin{x}}{x}~dx=\frac{\sin{y_n}}{y_n}\frac{\sin{n}}{n}$ for some $0\leq y_n\leq\frac{\sin{n}}{n}$. What can you deduce? What du you know about the behaviour of $\frac{\sin{x}}{x}$ near $0$?

Determine if $\sum^{\infty}_{n=1}\int^{\frac{\sin n}{n}}_0\frac{\sin x}{x} \, dx $ is converges or diverges.

4 Answers4