Let $V$ be a finite-dimensional inner product space over $R$ and suppose $f: V\rightarrow V$ is a rigid motion.
Prove that $f$ is both injective and surjective.
So I know that a rigid motion is an isometry and is defined by the function $f: V\rightarrow V$ such that $||f(x) - f(y)|| = ||x - y||$ for all $x,y\in V$, where $V$ is an inner product space.
I'm struggling to figure out how to prove injectivity and surjectivity using that definition.
Any guidance on how to prove this?
Checking injectivity is straighfroward: if $v\neq w$, then $\lVert f(v)-f(w)\rVert = \lVert v-w\rVert \neq 0$, hence $f(v)\neq f(w)$. This proves injectivity.
Proving surjectivity seems to me to be trickier; can't think of a way right now other than going the long way around: using the fact that a rigid motion that fixes $0$ is linear.
So say $f$ is a rigid motion. Then so is $g(x) = f(x)-f(0)$, because it's a rigid motion followed by a translation. But $g(0)=0$, so $g$ is actually linear. And since $g$ is one-to-one linear on a finite dimensional vector space, it is also onto. But if $g$ is onto, then so is $f$.
(I suspect there may be a clever way of showing it is onto, but finite-dimensionality needs to play a role and I can't come up with it right now).
If $\ g(x)=f(x)-f(0)\ $ then $\ g\ $ must be an orthogonal linear transformation. Here's an outline of a proof.
First, $$ \|g(x)\|=\|f(x)-f(0)\|=\|x\|\ , $$ and \begin{align}\|g(x)-g(y)\|^2&=\|f(x)-f(0)-(f(y)-f(0))\|^2\\&=\|x-y\|^2\\ &=\|x\|^2+\|y\|^2-2\langle x,y\rangle\ , \end{align} but \begin{align}\|g(x)-g(y)\|^2&=\|g(x)\|^2+\|g(y)\|^2-2\langle g(x),g(y)\rangle\\ &=\|x\|^2+\|y\|^2-2\langle g(x),g(y)\rangle\ . \end{align} Therefore $$ \langle g(x),g(y)\rangle=\langle x,y\rangle\ . $$ Now \begin{align} \langle g(x)&,g(\lambda y+\mu z)-\lambda g(y)-\mu g(z)\rangle\\ &=\langle g(x),g(\lambda y+\mu z)\rangle-\lambda\langle g(x),g(y)\rangle-\mu\langle g(x),g(z)\rangle\\ &=\langle x,\lambda y+\mu z\rangle-\lambda\langle x,y\rangle-\mu\langle x,z\rangle\\ &=0\ . \end{align} Since this is holds for any $\ x\ $, we have, in particular, \begin{align} \langle g(\lambda y+\mu z),g(\lambda y+\mu z)-\lambda g(y)-\mu g(z)\rangle&=0\ ,\\ \langle g(y),g(\lambda y+\mu z)-\lambda g(y)-\mu g(z)\rangle&=0\ ,\ \text{and}\\ \langle g(z),g(\lambda y+\mu z)-\lambda g(y)-\mu g(z)\rangle&=0\ , \end{align} and therefore \begin{align} &\|g(\lambda y+\mu z)-\lambda g(y)-\mu g(z)\|^2\\ &=\langle g(\lambda y+\mu z)-\lambda g(y)-\mu g(z),g(\lambda y+\mu z)-\lambda g(y)-\mu g(z)\rangle\\ &=\langle g(\lambda y+\mu z),g(\lambda y+\mu z)-\lambda g(y)-\mu g(z)\rangle\\ &\hspace{1em}-\lambda\langle g(y),g(\lambda y+\mu z)-\lambda g(y)-\mu g(z)\rangle\\ &\hspace{1em}-\mu\langle g(z),g(\lambda y+\mu z)-\lambda g(y)-\mu g(z)\rangle\\ &=0\ . \end{align} It follows that $\ g(\lambda y+\mu z)=\lambda g(y)+\mu g(z)\ $, and so $\ g\ $ is linear. Since $\ g(x)=0\ $ implies that $$ \|x\|=\|g(x)\|=0\ , $$ and hence that $\ x=0\ $, it follows that $\ \ker g=\{0\}\ $, and so $\ g\ $ is injective. It then follows from the rank-nullity theorem for finite dimensional spaces that $\ g\ $ is also surjective.
Thus, if $\ f(x)=f(y)\ $, then $\ g(x)=$$f(x)-f(0)=$$f(y)-f(0)=$$g(y)\ $, which implies $\ x=y\ $. So $\ f\ $ is also injective. And if $\ z\in V\ $, and $\ y=g^{-1}(z-f(0))\ $, then $\ f(y)=g(y)+f(0)=z\ $, so $\ f\ $ is also surjective.
@lonzaleggiera gave an excellent "algebraic proof" (+1). Here are two alternative arguments: one geometric and one topological. The topological one is noteworthy as it takes a different route to most solutions, by not showing that any maps are linear. However it uses invariance of domain instead, which is actually less trivial to prove than linearity. Credit for the topological solution to @PhoemueX for the comment here. Variants of this question have been asked so many times I expect someone has also posted the geometric solution too, at some point. In my view the one by @lonzaleggiera is the best of these 3, as it is the most succinct and self-contained, but the others are interesting in their own right.
Solution $2$ (Geometric): Let $V$ be a finite dimensional real vector space with Euclidean norm. Suppose that $g$ is a rigid motion of $V$, fixing the origin $O$. We will show that $g$ is linear. Bijectivity of an arbitrary rigid motion follows.
The vectors $Z$ in the line segment $XY$ are characterized by the condition $||X-Y|| =||X-Z|| + ||Z-Y||$, so $g$ preserves line segments.
Let $\lambda\geq1$ and $X\in V$. Then $Y=\lambda g(X)$ is the unique vector satisfying $||Y||=\lambda||X||$ and $g(X)$ lies on the line segment $OY$.
As $X$ lies on the line segment $O(\lambda X)$, we know $g(X)$ lies on the line segment $O(g(\lambda X))$. Further we know $||g(\lambda X)||=\lambda||X||$. Thus $g(\lambda X)=\lambda g(X)$.
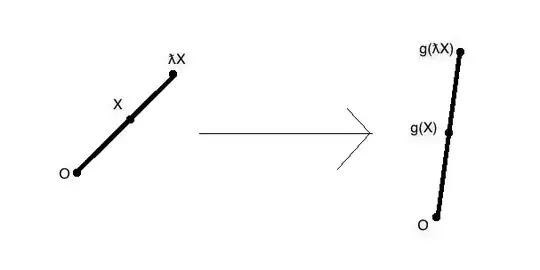
The cases $\lambda\leq0$ and $\lambda\in (0,1)$ follow analogously.
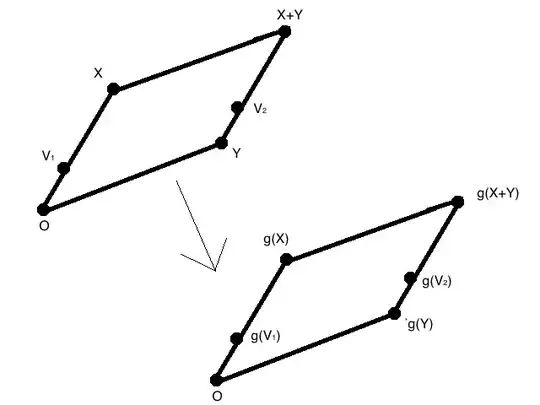
Now consider a pair of vectors $X,Y$. We have a parallelogram $OX(X+Y)Y$. Thus for $\delta\in (0,||X||)$, if $V_1$ lies in the line segment $OX$, at distance $\delta$ from $O$, and $V_2$ lies in the line segment $Y(X+Y)$, at distance $\delta$ from $Y$, then $||V_1-V_2||=||Y||$.
Applying $g$ to this configuration, we must obtain a parallelogram $O(g(X))(g(X+Y))(g(Y))$, as $||g(V_1)-g(V_2)||=||g(Y)||$, for all $\delta\in (0,||X||)$. Thus $g(X+Y)=g(X)+g(Y)$.
Solution 3 (Topological): Let $V$ be a finite dimensional real vector space with Euclidean norm. Suppose that $f$ is a rigid motion of $V$. Then $f$ is clearly injective and continuous, and im$(f)$ is non-empty.
Let $Y$ be an accumulation point of im$(f)$. Then we have a sequence of vectors $X_i\in V$ with $f(X_i)\to Y$ and $f(X_i)$ Cauchy, so $X_i$ is Cauchy. Let $X_i\to X$. Then by continuity, $f(X)=Y$, so im$(f)$ is closed.
By invariance of domain we also know that im$(f)$ is open. As it is also non-empty, by connectedness of $V$ we have that im$(f)$ is the whole of $V$.
