Finding the anti-derivative of $ \frac{e^{-c y^2 }}{y\sqrt{y^2-1}}$

Question

I am trying to evaluate the integral \begin{align} \frac{1}{2\sqrt{2}\pi}\int_{0^{-}}^{t} ds \ \frac{e^{-x^2/2S^2(t,s) }}{\Sigma(s) S(t,s)} \end{align} where $S(t, s) = 2D(t-s)+\frac{\Sigma(s)}{2}$ and $\Sigma(s)= \sigma^2+2Ds$. I found a rather neat change of variable by taking $\xi=S^{-1}(t,s)$ so that \begin{align} \Sigma(s)&=\sqrt{2} \ \xi^{-1}\sqrt{\xi^2\Sigma^2(t)-1}\\ 2D(t-s)&=2 \ \xi^{-2}-\Sigma^2(t)\\ ds&=\frac{2}{D\xi^3}\ d\xi \end{align} Applying this to the integral gives the result \begin{align} \frac{1}{2 \pi D}\int_{\sqrt{2}/\Sigma (2 t)}^{\sqrt{2}/\Sigma (t)} d{\xi} \ \frac{e^{-x^2 \ \xi^2/2 }}{\xi\sqrt{\Sigma^2(t)\xi^2-1}}=\frac{1}{2 \pi D}{\int_{\xi_L}^{\xi_H} d{\xi} \frac{e^{-x^2 \ \xi^2/2 }}{\xi\sqrt{\Sigma^2(t)\xi^2-1}}}. \end{align} and at last applying the change of variable $y=\Sigma(t)\xi$ gives \begin{align} \frac{1}{2 \pi D}{\int_{\xi_L}^{\xi_H} d{\xi} \frac{e^{-x^2 \ \xi^2/2 }}{\xi\sqrt{\Sigma^2(t)\xi^2-1}}} = \frac{1}{2 \pi D}{\int_{\sqrt{2}\Sigma(t)/\Sigma(2t)}^{\sqrt{2}} d{y} \frac{e^{-(x^2/2\Sigma^2(t)) y^2 }}{y\sqrt{y^2-1}}} =\frac{1}{2 \pi D}\color{blue}{\int_{a}^{b} d{y} \frac{e^{-c y^2 }}{y\sqrt{y^2-1}}} \end{align} Above calculation indeed check out numerically. 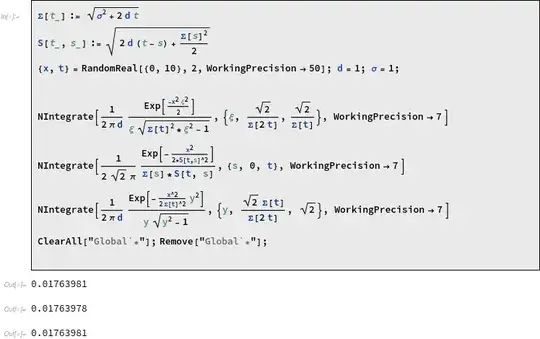It seems the integral in blue could have an anti-derivative. However, no luck just yet! Someone who knows a way forward? Many thanks in advance!

Answer 1

As others have pointed out, no closed-form solution in terms of elementary functions can be found. However, if you can live with the error function and the Owen T function then a closed-form solution can be found in terms of these special functions.

I will assume the error function $\operatorname{erf} (x)$ is well known to you. An integral representation for the Owen T function we intent to use can be found here. It is $$\operatorname{T}(h,a) = \frac{1}{2\sqrt{2\pi}} \int_h^\infty e^{-x^2/2} \operatorname{erf} \left (\frac{ax}{\sqrt{2}} \right )\, dx.$$ Enforcing a substitution of $x \mapsto x \sqrt{2}$ gives the following form that will be found most convenient for the integral considered here: $$\int_z^\infty e^{-x^2} \operatorname{erf}(ax) \, dx = 2 \sqrt{\pi} \operatorname{T}(z \sqrt{2}, a). \tag1$$

Now let us look at the integral in question. Let $$I(t) = \int_a^b \frac{e^{-tx^2}}{x\sqrt{x^2 - 1}} \, dx, \quad t > 0.$$ I will assume $1 < a < b = \sqrt{2}$. Note that $I(\infty) = 0$ and we are required to find $I(c)$ where $c > 0$. Using Feynman's trick of differentiating under the integral sign with respect to $t$ gives $$I'(t) = - \int_a^b \frac{x e^{-tx^2}}{\sqrt{x^2 - 1}} \, dx.$$ Enforcing a substitution of $u^2 = x^2 - 1$ yields \begin{align*} I'(t) &= e^{-t} \int_{\alpha_1}^{\alpha_2} e^{-tu^2} \, du = -\frac{\sqrt{\pi} e^{-t}}{2\sqrt{t}} \operatorname{erf}(u\sqrt{t}) \Big{|}_{\alpha_1}^{\alpha_2}\\ &= -\frac{\sqrt{\pi} e^{-t}}{2\sqrt{t}} \left [\operatorname{erf}(\alpha_2 \sqrt{t}) - \operatorname{erf}(\alpha_1 \sqrt{t}) \right ]. \end{align*} Here $\alpha_1 = \sqrt{a^2 - 1}$ and $\alpha_2 = \sqrt{b^2 - 1}$.

Now, as $$\int_c^\infty I'(t) \, dt = I(\infty) - I(c) = -I(c),$$ since $I(\infty) = 0$, we have $$I(c) = -\frac{\sqrt{\pi}}{2} \int_c^\infty \frac{e^{-t}}{\sqrt{t}} \left [\operatorname{erf} \left (\alpha_2 \sqrt{t} \right ) - \operatorname{erf} \left (\alpha_1 \sqrt{t} \right ) \right ] \, dt.$$ On enforcing a substitution of $t \mapsto t^2$ one obtains $$I(c) = \sqrt{\pi} \int_{\sqrt{c}}^\infty e^{-t^2} \left [\operatorname{erf}(\alpha_2 t) - \operatorname{erf}(\alpha_1 t) \right ] \, dt.$$ Evaluating this integral in terms of the Owen T function, from (1) one immediately sees that $$I(c) = 2\pi \left (\operatorname{T} \left (\sqrt{2c}, \alpha_2 \right ) - \operatorname{T} \left (\sqrt{2c}, \alpha_1 \right ) \right ),$$ or $$\int_a^b \frac{e^{-cy^2}}{y\sqrt{y^2 - 1}} \, dy = 2\pi \left (\operatorname{T} \left (\sqrt{2c}, \sqrt{b^2 - 1} \right ) - \operatorname{T} \left (\sqrt{2c}, \sqrt{a^2 - 1} \right ) \right ),$$ the required closed-form expression for our integral.

Note, if $b = \sqrt{2}$, as it appears to be from the question, further simplification of one of the Owen T functions is possible. As can be seen here when the right argument of the Owen T function is unity $$\operatorname{T} \left (\sqrt{2c}, \sqrt{b^2 - 1} \right ) = \operatorname{T} \left (\sqrt{2c}, 1 \right ) = \frac{1}{8} \left [1 - \operatorname{erf}^2 \left (\sqrt{c} \right ) \right ],$$ allowing one to write $$\int_a^{\sqrt{2}} \frac{e^{-cy^2}}{y\sqrt{y^2 - 1}} \, dy = -\frac{\pi}{4} \left [8 \operatorname{T} \left (\sqrt{2c}, \sqrt{a^2 - 1} \right ) + \operatorname{erf}^2 \left (\sqrt{c} \right ) - 1 \right ].$$

Answer 2

If $$f(x)=\frac{e^{-x^2}}{x\sqrt{x^2-1}}$$ then the integral $I=\int_a^bf(x)dx, b>a$ is not only convergent for all $a>a_0$ where $a_0$ is the root of $1/x=f(x)$, but also $f(x)\in[0,1)$, which gives a hope of some closed form of the definite integral. At least, a very close approximant. Like, the transformation $x=\sec t$ gives for the integral $$\int_\alpha^\beta e^{-\sec^2t}dt$$. A silver lining of hope.

EDIT

If we consider $E(x)=\int_0^x e^{-\sec^2t}dt$, although the Taylor expansion is a little hopeless: $$ e^{-\sec^2x} = \frac{1}{e} \left( 1 - x^2 - \frac{1}{6}x^4 + \frac {11}{90}x^6+O (x^8)\right) $$ The denominators are the sequence $$a_n = \frac{(2n)!}{2^n} $$, and I'm not sure of the numerators. Yet, via some graphing it can be seen that the following is approximately correct. $$ e^{-\sec^2x} \approx e^{-1-x^2}(1-\alpha x^4), \text{where } \alpha \in \left[ \frac{2}{3},\frac{5}{6} \right] $$ Therefore, a crude approximation, $$E(x)=\frac {\sqrt\pi}{8e}(4-3\alpha) \text{erf} (x) + e^{-1-x^2} \left( \frac{x^3}{2} +\frac{3x}{4} \right) $$

Answer 3

The integral in question doesn't have an elementary anti-derivative for all $c$. For example, consider the case where $c=1$:

$$I = \int_1^{\sec{x}} \dfrac{e^{-y^2}}{y\sqrt{y^2-1}} \textrm{d}y$$

By making the substitution $y=\sec{t}$, we may observe the following:

$$I = \int_0^x e^{-\sec^2t} \textrm{d}t$$

Now, I don't know much about this new integral, but I do know that $$I = \int_0^{\frac{\pi}{2}n} e^{-\sec^2t} \textrm{d}t = \dfrac{\pi}{2}n \left(1-\textrm{erf}(1)\right)$$ which gives me the feeling that the integral which you are trying to solve is non-elementary.

Answer 4

Firstly, $$I(z,c)=\int\limits_z^{\sqrt2} \dfrac{e^{-cy^2}\,\text dy}{y\sqrt{y^2-1}} =e^{-c}\int\limits_z^{\sqrt2}\dfrac{e^{-c(y^2-1)}}{y^2}\,\text d\sqrt{y^2-1} = e^{-c}\int\limits_{\sqrt{z^2-1}}^1 \dfrac{e^{-ct^2}\,\text dt}{t^2+1}.\tag1$$

At the second, are known the integrals $$\int\limits_0^\infty \dfrac{e^{-ct^2}\,\text dt}{t^2+1}\,\text dt = \dfrac\pi2 e^c\operatorname{erfc}\sqrt c,\tag2$$ $$\int\limits_0^1 \dfrac{e^{-ct^2}\,\text dt}{t^2+1}\,\text dt = \dfrac\pi4 e^c\left(1-\operatorname{erfc}^2\sqrt c\right),\tag3$$ with the closed form of $$I(1,c)=\dfrac\pi4\left(1-\operatorname{erfc}^2\sqrt c\right).\tag4$$

Besides, $$\int\limits_0^a \dfrac{t^{2k}\,\text dt}{t^2+1}\,\text dt = -\dfrac i2 (-1)^k \operatorname{B}\left(-a^2,k+\dfrac12,0\right),\tag5$$

$$\int\limits_0^a \dfrac{e^{-ct^2}\,\text dt}{t^2+1}\,\text dt = \sum\limits_{k=0}^\infty (-c)^k\int\limits_0^a \dfrac{t^{2k}\,\text dt}{t^2+1}\,\text dt =-\dfrac i2 \sum_{k=0}^\infty c^k\operatorname{B}\left(-a^2,k+\dfrac12,0\right),\tag6$$

$$I(z,c)=I(1,c)-e^{-c}\int\limits_0^{\sqrt{z^2-1}} \dfrac{e^{-ct^2}\,\text dt}{t^2+1}\,\text dt,\tag7$$ $$I(z,c)=I(1,c) + \dfrac i2 e^{-c} \sum_{k=0}^\infty c^k \operatorname{B}\left(1-z^2,k+\dfrac12,0\right).\tag8$$

Therefore, in the common case the given integral $(1)$ can be presented by the series $(8),$ which is not a closed form.