On $\mathrm{\sum\limits_{n=0}^\infty \left(C(n)-\frac{\sqrt\pi}{2\sqrt2}\right)+ \sum\limits_{n=0}^\infty \left(S(n)-\frac{\sqrt\pi}{2\sqrt2}\right)}$

Question

This question will take inspiration from

Evaluation of $\sum\limits_{n=0}^\infty \left(\operatorname{Si}(n)-\frac{\pi}{2}\right)$?

and

On $\mathrm{\sum\limits_{x=1}^\infty Ci(x)}=\frac{\ln(2)+\ln(\pi)-γ}{2}$

The problem will include the version with the Fresnel integrals. The separate sums converge to a similar value each, but converge slowly due to oscillation. Note there are also hypergeometric function representations, but these probably are not useful for evaluation. F(x) is the Dawson Integral function. I will not put more representations as they can easily be found in the link. The other representations are just as complicated. Here are the definitions:

$$\mathrm{C(x)=\int cos\left(x^2\right)dx, S(x)=\int sin\left(x^2\right)dx, \lim_{x\to\infty} C(x), S(x)= \frac{\sqrt\pi}{2\sqrt2} }$$

so the function is asymptotic to $\frac{\sqrt\pi}{2\sqrt2}$ and the following follow from it:

$$\mathrm{\sum_{n=0}^\infty \left(C(n)-\frac{\sqrt\pi}{2\sqrt2}\right)+\sum_{n=0}^\infty \left(S(n)-\frac{\sqrt\pi}{2\sqrt2}\right)=-\sqrt{\frac\pi2}+\sum_{n=1}^\infty \left(C(n)+S(n)-\sqrt{\frac\pi 2}\right)=\sum_{n=0}^\infty \left( \frac{(1 - i) \left(F\left( (-1 + i) n\right) - i\,F\left((1 + i) n \right) e^{2 i π n^2 }\right)}{e^{in^2}}+ \frac{(1 - i) \left(F\left((-1 + i)n\right) - i\,F\left((1 + i) n\right) e^{i π n^2}\right)}{e^{ i n^2 }}-\sqrt{\frac\pi 2}\right)=log_b\prod_{n=0}^\infty b^{C(n)+S(n)-\sqrt{\frac\pi2}}}$$

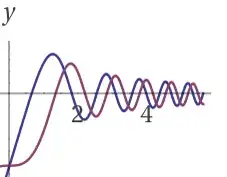
Here is what each individual summand looks like using the problem’s definitions. The blue plot is the cosine version and the purple is the sine version:

There are also sum to integral representation formulas like the Abel-Plana formulas. This one may work with the Abel-Plana formula:

$$\mathrm{\sum_{n=0}^\infty \left(C(n)-\frac{\sqrt\pi}{2\sqrt2}\right)+\sum_{n=0}^\infty \left(S(n)-\frac{\sqrt\pi}{2\sqrt2}\right)=-\frac12 \frac{\sqrt\pi}{2\sqrt2} +\int_0^\infty C(x)-\frac{\sqrt\pi}{2\sqrt2}dx +i\int_0^\infty\frac{C(ix)-\frac{\sqrt\pi}{2\sqrt2}-C(-ix)- -\frac{\sqrt\pi}{2\sqrt2}}{e^{2\pi x}-1}-\frac{\sqrt\pi}{2\sqrt2} \frac12+\int_0^\infty S(x)-\frac{\sqrt\pi}{2\sqrt2} dx+ i\int_0^\infty\frac{S(ix)-\frac{\sqrt\pi}{2\sqrt2}-S(-ix)- -\frac{\sqrt\pi}{2\sqrt2}}{e^{2\pi x}-1}= 2\int_0^\infty \frac{S(x)}{e^{2\pi x}-1}dx-2\int_0^\infty\frac{C(x)}{e^{2\pi x}-1}dx-\frac12 -\frac{\sqrt{\pi}}{2\sqrt2}}$$

Another idea is to use the main power series definition of the Fresnel Integrals seen in the bolded link:

$$\mathrm{\sum\limits_{n=0}^\infty \left(C(n)-\frac{\sqrt\pi}{2\sqrt2}\right)+ \sum\limits_{n=0}^\infty \left(S(n)-\frac{\sqrt\pi}{2\sqrt2}\right)= \sum\limits_{x=0}^\infty \left(-\sqrt\frac{\pi}{2}+\sum_{n=0}^\infty\left(\frac{(-1)^n x^{4n+3}}{(2n+1)!(4n+3)}+\frac{(-1)^nx^{4n+1}}{(2n)! (4n+1)}\right)\right)}$$

Using this Imaginary Error function definition, one other idea is to notice that:

$$\mathrm{(-1)^{\frac74} \frac{\sqrt{\pi} }{2}\,erfi\left(\sqrt[4]{-1} x\right)=C(x)+i\,S(x)=\int e^{ix^2}dx\implies \sum\limits_{n=0}^\infty \left(C(n)-\frac{\sqrt\pi}{2\sqrt2}\right)+ \sum\limits_{n=0}^\infty \left(S(n)-\frac{\sqrt\pi}{2\sqrt2}\right)= Re\sum_{x=0}^\infty \left((-1)^{\frac74} \frac{\sqrt{\pi} }{2}\,erfi\left(\sqrt[4]{-1} x\right)-\frac{\sqrt\pi}{2\sqrt2}(1+i)\right)+Im \sum_{x=0}^\infty \left((-1)^{\frac74} \frac{\sqrt{\pi} }{2}\,erfi\left(\sqrt[4]{-1} x\right)-\frac{\sqrt\pi}{2\sqrt2}(1+i)\right)=}$$

This means that an equivalent summation to find is the following. Let’s try to use the Abel-Plana formula on it:

$$\mathrm{\sum_{x=0}^\infty \left((-1)^{\frac74} \frac{\sqrt{\pi} }{2}\,erfi\left(\sqrt[4]{-1} x\right)-\frac{\sqrt\pi}{2\sqrt2}(1+i)\right)= -\frac{\frac12\sqrt\pi}{2\sqrt 2}(1+i)+\int_0^\infty (-1)^{\frac74} \frac{\sqrt{\pi} }{2}\,erfi\left(\sqrt[4]{-1} x\right)-\frac{\sqrt\pi}{2\sqrt2}(1+i)dx +i\int_0^\infty \frac{(-1)^{\frac74} \frac{\sqrt{\pi} }{2}\,erfi\left(\sqrt[4]{-1} ix\right)-\frac{\sqrt\pi}{2\sqrt2}(1+i)-(-1)^{\frac74} \frac{\sqrt{\pi} }{2}\,erfi\left(\sqrt[4]{-1} -ix\right)+\frac{\sqrt\pi}{2\sqrt2}(1+i)}{e^{2\pi x}-1}dx= -\frac{\sqrt\pi}{4\sqrt 2}(1+i)+\frac i2 +(-1)^\frac34 \sqrt\pi\int_0^\infty\frac{erf\left(\sqrt[4]{-1}x\right)}{e^{2\pi x}-1}≈.65507…+.86175…i}$$

Note there may be a typo. How can I evaluate this integral or summation? Please correct me and give me feedback!

Answer 1

This answer is based on the Abel-Plana formula

---

$$\sum\limits_{n=0}^\infty f(n)=\int\limits_0^\infty f(x)\,dx+\frac{1}{2}f(0)+i\int\limits_0^\infty\frac{f(i t)-f(-i t)}{e^{2 \pi t}-1}\,dt\tag{1}$$

---

where

---

$$f(x)=C(x)+S(x)-\sqrt{\frac{\pi}{2}}\tag{2}$$

$$C(x)=\int\limits_0^x\cos\left(t^2\right)\,dt\tag{3}$$

$$S(x)=\int_\limits0^x\sin\left(t^2\right)\,dt\tag{4}$$

---

which leads to

---

$$\sum\limits_{n=0}^\infty\left(C(n)+S(n)-\sqrt{\frac{\pi}{2}}\right)=\int_0^\infty\left(C(x)+S(x)-\sqrt{\frac{\pi}{2}}\right)\,dx+\frac{1}{2}\left(C(0)+S(0)-\sqrt{\frac{\pi}{2}}\right)+i\int_0^\infty\frac{C(i t)+S(i t)-\sqrt{\frac{\pi}{2}}-\left(C(-i t)+S(-i t)-\sqrt{\frac{\pi}{2}}\right)}{e^{2 \pi t}-1}\,dt\ .\tag{5}$$

---

Based on the identities $C(i t)=i\,C(t)$, $S(i t)=-i\,S(t)$, $C(-i t)=-i\,C(t)$, and $S(-i t)=i\,S(t)$ and noting that $\frac{1}{2}\left(C(0)+S(0)-\sqrt{\frac{\pi}{2}}\right)=-\frac{1}{2}\sqrt{\frac{\pi }{2}}$ formula (5) above simplifies to formula (6) below.

---

$$\sum\limits_{n=0}^\infty\left(C(n)+S(n)-\sqrt{\frac{\pi}{2}}\right)=\int\limits_0^\infty\left(C(x)+S(x)-\sqrt{\frac{\pi}{2}}\right)\,dx-\frac{1}{2}\sqrt{\frac{\pi}{2}}+2\int\limits_0^\infty\frac{S(t)-C(t)}{e^{2 \pi t}-1}\,dt\tag{6}$$

---

Observational convergence of $\int_0^y\left(C(x)+S(x) -\sqrt{\frac \pi 2}\right) dx\to -\frac{1}{2}$ as $y\to\infty$ leads to formula (7) below.

---

$$\underset{K\to \infty}{\text{lim}}\left(\sum\limits_{n=0}^K\left(C(n)+S(n)-\sqrt{\frac{\pi}{2}}\right)\right)=-\frac{1}{2}-\frac{1}{2}\sqrt{\frac{\pi}{2}}+2\int\limits_0^\infty\frac{S(t)-C(t)}{e^{2 \pi t}-1}\,dt\tag{7}$$

---

The integral in formula (7) above can be evaluated using the identity

---

$$\frac{1}{e^{2 \pi t}-1}=\sum\limits_{n=1}^{\infty} e^{-2 \pi n t}\tag{8}$$

---

which leads to the following series representation.

---

$$2\int\limits_0^\infty\frac{S(t)-C(t)}{e^{2 \pi t}-1}\,dt=\underset{N\to \infty}{\text{lim}}\left(\frac{1}{\pi}\sum\limits_{n=1}^N\frac{\left(\cos\left(\pi^2 n^2\right)-\sin\left(\pi^2 n^2\right)\right)S(\pi n)-\left(\cos\left(\pi^2 n^2\right)+\sin\left(\pi^2 n^2\right)\right)C(\pi n)+\sqrt{\frac{\pi}{2}} \sin\left(\pi^2 n^2\right)}{n}\right)\tag{9}$$

---

The following table illustrates evaluation of the right side of formula (7) above using formula (9) above for several values of the upper evaluation limit $N$. The evaluations in the table below are consistent with evaluation of the right side of formula (7) above using numerical integration.

---

Table (1): Evaluation of the right side of formula (7) using formula (9)

$$\begin{array}{cc} \text{N} & \text{Formula (7)} \\ 10 & -1.20211 \\ 100 & -1.20643 \\ 1000 & -1.20688 \\ 10000 & -1.20693 \\ 100000 & -1.20693 \\ \end{array}$$

---

However there seems to be an unresolved discrepancy between evaluation of the right side of formula (7) above using numerical integration (or using the series representation of the integral defined in formula (9) above) and the following table which illustrates evaluation of the left side of formula (7) above using several values of the upper evaluation limit $K$.

---

Table (2): Evaluation of the left side of formula (7)

$$\begin{array}{cc} \text{K} & \text{Formula (7)} \\ 10 & -1.35553 \\ 100 & -1.52682 \\ 1000 & -1.52359 \\ 10000 & -1.51426 \\ 100000 & -1.51101 \\ \end{array}$$

---

Separating formula (2) for $f(x)$ into the two functions

---

$$f_c(x)=C(x)-\frac{1}{2}\sqrt{\frac{\pi}{2}}\tag{10}$$

$$f_s(x)=S(x)-\frac{1}{2}\sqrt{\frac{\pi}{2}}\tag{11}$$

---

where $f(x)=f_c(x)+f_s(x)$ leads to

---

$$\sum\limits_{n=0}^\infty\left(C(n)-\frac{1}{2}\sqrt{\frac{\pi}{2}}\right)=-\frac{1}{4}\sqrt{\frac{\pi}{2}}-2\int\limits_0^\infty\frac{C(t)}{e^{2 \pi t}-1}\,dt\tag{12}$$

$$\sum\limits_{n=0}^\infty\left(S(n)-\frac{1}{2}\sqrt{\frac{\pi }{2}}\right)=-\frac{1}{2}-\frac{1}{4}\sqrt{\frac{\pi}{2}}+2\int\limits_0^\infty\frac{S(t)}{e^{2 \pi t}-1}\,dt\tag{13}$$

---

where the two integrals can be evaluated as

---

$$-2\int\limits_0^\infty\frac{C(t)}{e^{2 \pi t}-1}\,dt=\underset{N\to \infty}{\text{lim}}\left(\frac{1}{\pi}\sum\limits_{n=1}^N\frac{\sin\left(\pi^2 n^2\right)\left(\frac{1}{2}\sqrt{\frac{\pi}{2}}-C(\pi n)\right)+\cos\left(\pi^2 n^2\right)\left(S(\pi n)-\frac{1}{2}\sqrt{\frac{\pi}{2}}\right)}{n}\right)\tag{14}$$

$$2\int\limits_0^\infty\frac{S(t)}{e^{2 \pi t}-1}\,dt=\underset{N\to \infty}{\text{lim}}\left(-\frac{1}{\pi}\sum\limits_{n=1}^N\frac{\cos\left(\pi^2 n^2\right)\left(C(\pi n)-\frac{1}{2}\sqrt{\frac{\pi}{2}}\right)+\sin\left(\pi^2 n^2\right)\left(S(\pi n)-\frac{1}{2}\sqrt{\frac{\pi}{2}}\right)}{n}\right)\tag{15}$$

---

Note the sum of formulas (12) and (13) above is consistent with formula (7) above, and the sum of formulas (14) and (15) above is consistent with formula (9) above.

---

The following table illustrates evaluations of the right sides of formulas (12) and (13) above using formulas (14) and (15) above for several values of the upper evaluation limit $N$. The evaluations in the table below are consistent with evaluations of the right sides of formulas (12) and (13) above using numerical integration. Note the right column of the table below is consistent with the evaluations in the corresponding Table (1) above.

---

Table (3): Evaluations of the right sides of formulas (12) and (13) using formulas (14) and (15)

$$\begin{array}{cccc} \text{N} & \text{Formula (12)} & \text{Formula (13)} & \text{Sum of Formulas (12) and (13)} \\ 10 & -0.391473 & -0.810639 & -1.20211 \\ 100 & -0.39579 & -0.810638 & -1.20643 \\ 1000 & -0.396243 & -0.810638 & -1.20688 \\ 10000 & -0.396289 & -0.810638 & -1.20693 \\ 100000 & -0.396293 & -0.810638 & -1.20693 \\ \end{array}$$

---

However there seems to be an unresolved discrepancy between evaluation of the right sides of formulas (12) and (13) above using numerical integration (or using the series representations of the integrals defined in formulas (14) and (15) above) and the following table which illustrates evaluations of the left sides of formula (12) and (13) above using several values of the upper evaluation limit $K$. Note the right column of the table below is consistent with the evaluations in the corresponding Table (2) above.

---

Table (4): Evaluations of the left sides of formulas (12) and (13)

$$\begin{array}{cccc} \text{K} & \text{Formula (12)} & \text{Formula (13)} & \text{Sum of Formulas (12) and (13)} \\ 10 & -0.63943 & -0.716102 & -1.35553 \\ 100 & -0.645717 & -0.881106 & -1.52682 \\ 1000 & -0.654904 & -0.86869 & -1.52359 \\ 10000 & -0.653089 & -0.861175 & -1.51426 \\ 100000 & -0.652134 & -0.858876 & -1.51101 \\ \end{array}$$