Find ellipse of maximum area which is entirely contained within the area defined by a set of points

Question

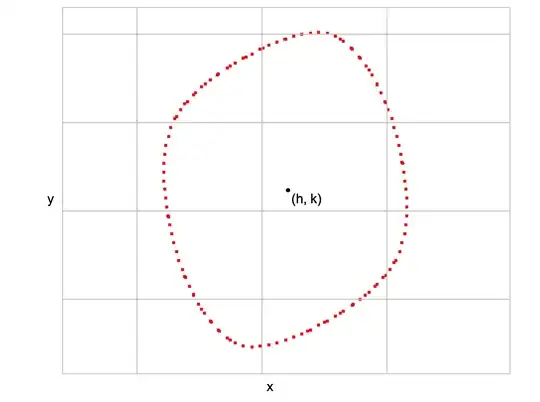
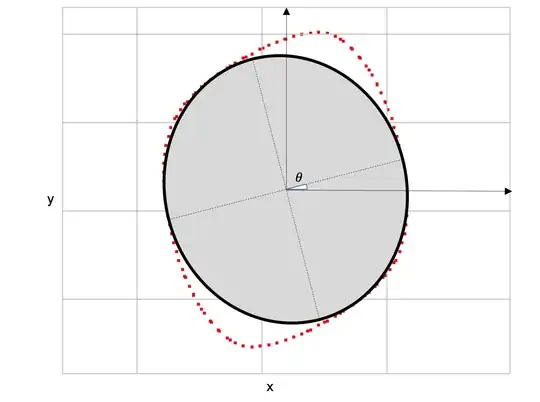
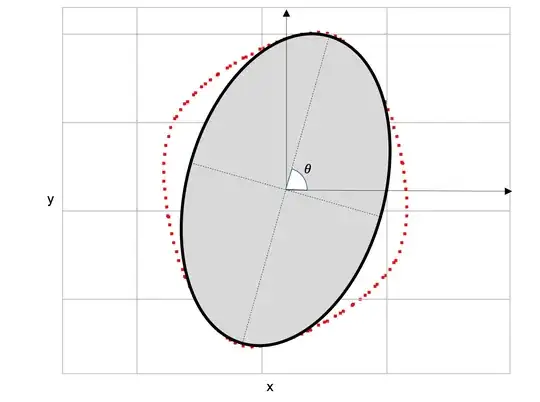
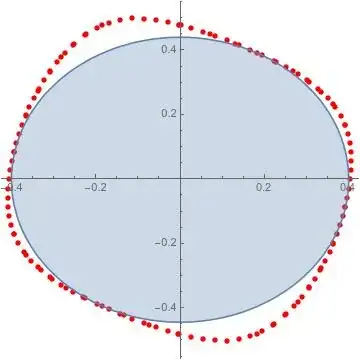
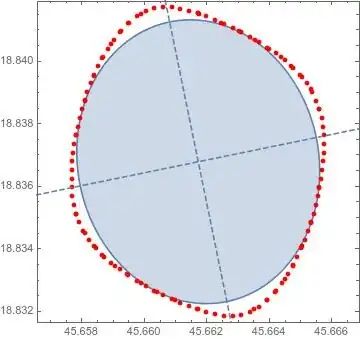
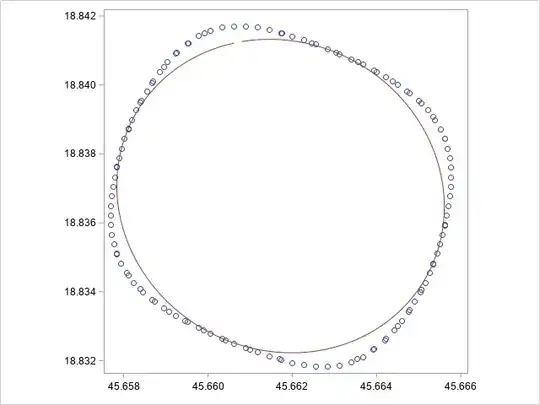
I have a set of $(x, y)$ coordinates, from which I would like to generate an ellipse of maximum possible area which is entirely contained within the area defined by the given points. The points are from contour lines and not given by an equation, but generally appear in the shape of skewed ellipses.

For example, for the following points,

x	y
45.66172222222225	18.841511212833733
45.66144444444447	18.841603609265974
45.661166666666695	18.84167023720114
45.66088888888892	18.841708840666733
45.66061111111114	18.841714721198922
45.66033333333336	18.8416792127312
45.66005555555558	18.841586913726573
45.659907959603544	18.8415
45.659777777777805	18.841432324588876
45.65952133520022	18.84122222222222
45.65950000000003	18.841205864567236
45.65925240431259	18.840944444444442
45.65922222222225	18.84091291427614
45.65903462855747	18.840666666666664
45.65894444444447	18.840543213692058
45.658848018922384	18.84038888888889
45.658686482591534	18.84011111111111
45.6586666666667	18.840075891391127
45.65854057470615	18.83983333333333
45.65841385937155	18.839555555555553
45.658388888888915	18.839497076739338
45.65829635419802	18.839277777777777
45.65819317225286	18.839
45.65811111111114	18.838743972287034
45.658103781273304	18.83872222222222
45.65801729926895	18.83844444444444
45.657943630825045	18.838166666666666
45.65788130483856	18.837888888888887
45.65783333333336	18.837633786630168
45.65782843965894	18.83761111111111
45.657777930516	18.83733333333333
45.65773797205481	18.837055555555555
45.65770846520107	18.836777777777776
45.65768983794373	18.836499999999997
45.65768315829199	18.836222222222222
45.657690315425526	18.835944444444443
45.657714290504025	18.835666666666665
45.65775954170573	18.835388888888886
45.65783252126027	18.83511111111111
45.65783333333336	18.835108788071842
45.65792541129527	18.834833333333332
45.65806060225678	18.834555555555553
45.65811111111114	18.834474038899852
45.65823358922209	18.834277777777775
45.658388888888915	18.834082623685447
45.658457173026996	18.834
45.6586666666667	18.833784998750474
45.658731945343874	18.83372222222222
45.65894444444447	18.83353762228444
45.65906160654751	18.833444444444442
45.65922222222225	18.83332268424614
45.65945121712184	18.833166666666664
45.65950000000003	18.833133439986426
45.659777777777805	18.83295712908462
45.659898642372674	18.83288888888889
45.66005555555558	18.832794864416265
45.66033333333336	18.832647295512253
45.66040951888557	18.83261111111111
45.66061111111114	18.832503587959618
45.66088888888892	18.832375253663077
45.66099358303661	18.83233333333333
45.661166666666695	18.832250897046737
45.66144444444447	18.83213848859703
45.66169543834408	18.832055555555552
45.66172222222225	18.832044342721858
45.66200000000003	18.831951946289568
45.6622777777778	18.83188531835439
45.662555555555585	18.83184671488883
45.66283333333336	18.831840834356605
45.663111111111135	18.831876342824323
45.66338888888892	18.831968641828965
45.663536484840996	18.832055555555552
45.66366666666669	18.83212323096666
45.663923109244294	18.83233333333333
45.663944444444475	18.832349690988305
45.66419204013188	18.83261111111111
45.66422222222225	18.832642641279445
45.66440981588704	18.83288888888889
45.664500000000025	18.83301234186348
45.664596425522106	18.833166666666664
45.664757961852935	18.833444444444442
45.66477777777781	18.833479664164482
45.664903869738325	18.83372222222222
45.66503058507293	18.834
45.66505555555558	18.834058478816264
45.66514809024647	18.834277777777775
45.66525127219165	18.834555555555553
45.66533333333336	18.834811583268447
45.66534066317122	18.834833333333332
45.66542714517556	18.83511111111111
45.66550081361947	18.835388888888886
45.66556313960594	18.835666666666665
45.66561111111114	18.83592176892534
45.66561600478556	18.835944444444443
45.665666513928514	18.836222222222222
45.66570647238968	18.836499999999997
45.665735979243436	18.836777777777776
45.665754606500776	18.837055555555555
45.66576128615252	18.83733333333333
45.66575412901897	18.83761111111111
45.665730153940466	18.837888888888887
45.665684902738775	18.838166666666666
45.66561192318422	18.83844444444444
45.66561111111114	18.83844676748368
45.665519033149245	18.83872222222222
45.66538384218772	18.839
45.66533333333336	18.8390815166557
45.66521085522241	18.839277777777777
45.66505555555558	18.83947293187009
45.66498727141749	18.839555555555553
45.66477777777781	18.83977055680508
45.664712499100624	18.83983333333333
45.664500000000025	18.84001793327112
45.66438283789701	18.84011111111111
45.66422222222225	18.840232871309414
45.66399322732267	18.84038888888889
45.663944444444475	18.840422115569137
45.66366666666669	18.840598426470944
45.66354580207184	18.840666666666664
45.66338888888892	18.84076069113929
45.663111111111135	18.840908260043292
45.663034925558904	18.840944444444442
45.66283333333336	18.841051967595934
45.662555555555585	18.84118030189247
45.66245086140788	18.84122222222222
45.6622777777778	18.841304658508818
45.66200000000003	18.8414170669585
45.66174900610049	18.8415
45.66172222222225	18.841511212833733

and given the centre of the points $(h, k)$,

And the equation for an ellipse that is not at the origin and is rotated by an angle (taken from the answers at What is the general equation of the ellipse that is not in the origin and rotated by an angle?),

$$\frac{((x−h)\cos(A)+(y−k)\sin(A))^2}{a^2}+\frac{((x−h)\sin(A)-(y−k)\cos(A))^2}{b^2}=1$$

I would like to calculate the variables $a$, $b$ (the semi-axes respectively) and $A$ (the angle of rotation of the ellipse from the x-axis) for an ellipse of the largest possible area, from which I will be able to construct an ellipse of the same size and angle at any point $(h, k)$.

My initial idea was to find the minimum radius of the area defined by the points and centred on $(h, k)$, then find the radius of the same area at an angle of 90 degrees from the minimum, but a very rough calculation appears to show that this will include some amount of area outside the boundary defined by the points. For the ellipse to fit within the points, the major axis must then be narrower than the total width of the area at that angle.

On the other hand, another possibility would be to find the maximum radius of the area defined by the points and centred on $(h, k)$, then find the radius of the same area at an angle of 90 degrees from the maximum, but once again this includes some amount of area outside the point boundary, and for the ellipse to fit within the points, the minor axis must then be narrower than the total width of the area at that angle.

It is difficult to tell which method will yield an ellipse of larger possible area by these rough plots, or if there is yet another superior method; so I ask, is there a method or algorithm to determine this analytically? If it is possible to use an equation for a skewed ellipse to cover an even larger area then that would be even better - the aim is to generate an equation for a shape covering the maximum amount of area defined by the points, to then be able to determine the width of the resulting shape at any angle.

Answer 1

NOTE - 1

We changed the original script to cope with some difficulties due to data scaling problems.

Assuming that the label data represents the data given in the proposed question, we follow with

g = Total[data]/Length[data]
data = Table[data[[k]] - g, {k, 1, Length[data]}];
X = Transpose[data][[1]];
Y = Transpose[data][[2]];
xmin = Min[X];
xmax = Max[X];
ymin = Min[Y];
ymax = Max[Y];
dX = xmax - xmin;
dY = ymax - ymin;
dXY = Max[dX, dY];
Xs = X/dXY;
Ys = Y/dXY;
datas = Transpose[{Xs, Ys}];
mu = 1
f[x_, y_] := b^2 ((x - x0) Cos[t] + (y - y0) Sin[t])^2 + a^2 ((x - x0) Sin[t] - (y - y0) Cos[t])^2 - a^2 b^2
restrs = Table[f[datas[[k, 1]], datas[[k, 2]]] >= 0, {k, 1, Length[datas]}];
obj = Join[{a b, a > 0, b > 0, x0^2 + y0^2 < (dX^2 + dY^2)/20, 0 < t < Pi, a <= mu, b <= mu}, restrs];
sol = NMaximize[obj, {a, b, x0, y0, t}]
restrs /. sol[[2]]
obj /. sol[[2]]
f0 = f[x, y] /. sol[[2]]
gr0 = ListPlot[datas, PlotStyle -> {Red, PointSize[0.02]}];
gr1 = RegionPlot[f0 <= 0, {x, -mu, mu}, {y, -mu, mu}];
Show[gr0, gr1, PlotRange -> All, AspectRatio -> 1]

Here we assume the ellipse equation as

$$ f(x,y,x_0,y_0,a,b) = b^2((x-x_0)\cos\theta+(y-y_0)\sin\theta)+a^2((x-x_0)\sin\theta-(y-y_0)\cos\theta)-a^2b^2=0 $$

and also the data points with origin at their barycenter: now, regarding the data points $(x_k,y_k)$ we impose as restrictions

$$ \mathcal{R}=\{f(x_k,y_k,x_0,y_0,a,b)\ge 0,\ \ \forall k\} $$

with additional restrictions to help the optimizer $\mu > a > 0,\mu > b > 0, \epsilon_1\le \theta\le \pi, x_0^2+y_0^2 \le \epsilon_2$ and finally we maximize the ellipse area which is proportional to $a b$.

NOTE - 2

We left to the reader the scale corrections in the ellipse coefficients, due to the factor dXY introduced to calculate Xs, Ys.

After re-scaling the solution is given by the ellipse

$$ 67279.5 (-0.979646 (x-45.6617)-0.200733 (y-18.8368))^2+47964. (0.979646 (y-18.8368)-0.200733 (x-45.6617))^2=1 $$

Answer 2

The (nonconvex nonlinear) problem of maximizing $\pi a b$ subject to \begin{align} \frac{((x_i−h)\cos A+(y_i−k)\sin A)^2}{a^2}+\frac{((x_i−h)\sin A-(y_i−k)\cos A)^2}{b^2} &\ge 1 &&\text{for all $i$} \tag1 \\ a&\ge b \tag2 \\ 0 \le A &\le \pi \tag3 \end{align} is unbounded, but you can impose $a \le d/2$, where $d$ is the diameter of the input set.

It is not clear from your description whether $h$ and $k$ are fixed or decision variables. If they are not fixed, you need additional (linear) constraints to force the center $(h,k)$ to be inside the polygon.

Here is a locally optimal solution for your sample data: $$h= 45.6617222, k= 18.8367778, A= 1.8217672, a= 0.0047061, b= 0.0037456$$