5

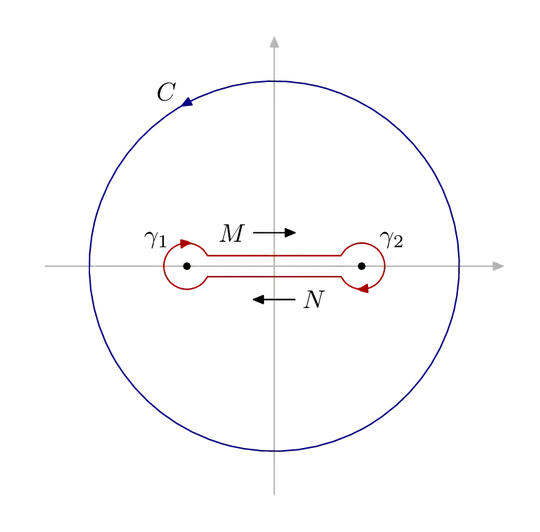
Can I evaluate $\int_{-1}^1\sqrt{1-x^2}dx=\pi/2$ by using complex integration? Using the dog bone contour it seems perfectly possible. But the function has no residue... Isn't the integral around the closed contour equal to zero?

(The dog bone contour is in red below) enter image description here

thedude
  • 1,777
  • The integrand isn't holomorphic on all domains, being a branch of the square root. What dog bone are you using: check you can pick a branch that is holomorphic on the closure of your region of integration. – user2628206 Aug 06 '21 at 13:01
  • 1
    the integral is on a line from -1 to 1, so not a closed contour –  Aug 06 '21 at 13:03
  • @river I mean the integral around the dog bone contour, that is closed – thedude Aug 06 '21 at 13:05
  • @user2628206 I don't understand what you mean. I am using the usual dog bone that goes around the branch line, which is between -1 and 1. Isn't the function holomorphic outside of that? – thedude Aug 06 '21 at 13:07
  • I don't know what the usual dog bone is, so I can't comment further, but It seems like you have taken branches into account and thus holomorphicity isn't the problem. Consider adding details about the curves you have set up, and then users can better understand your analysis and spot any potential problems in reasoning . – user2628206 Aug 06 '21 at 13:29
  • @user2628206 I have included an image of the dog bone contour in the question – thedude Aug 06 '21 at 13:34

2 Answers2

7

Since the integrand, $f(z)=\sqrt{1-z^2}$, is not analytic inside the dog bone contour, $C_{DB}=M+\gamma_2+N+\gamma_1$, Cauchy's integral theorem does not apply. However, inasmuch outside of $C_{DB}$ , $\sqrt{1-z^2}$ is indeed analytic, then we can assert that for any $R>1$

$$\begin{align} \oint_{C_{DB}} \sqrt{1-z^2}\,dz&=-\oint_{|z|=R}\sqrt{1-z^2}\,dz\tag1 \end{align}$$

where the negative sign that multiplies the integral on the right-hand side of $(1)$ is a consequence of the orientation.

NOTE:

To ensure that $\sqrt{1-x^2}\ge 0$ on $[-1,1]$ on the upper part of the branch cut, we have $\sqrt{1-z^2}=-i\sqrt{z^2-1}$. We use this relationship in the ensuing analysis.

We can proceed by writing

$$\begin{align} -\oint_{|z|=R}\sqrt{1-z^2}\,dz&=-\int_0^{2\pi}\sqrt{1-R^2e^{i2\phi}}\,iRe^{i\phi}\,d\phi\\\\ &=-R\int_0^{2\pi}e^{i\phi}\sqrt{R^2e^{i2\phi}-1}\,d\phi\\\\ &=-R^2\int_0^{2\pi}e^{i2\phi}\left(1-\frac{1}{R^2e^{i2\phi}}\right)^{1/2}\,d\phi\\\\ &=-R^2 \int_0^{2\pi}e^{i2\phi} \sum_{n=0}^\infty \binom{1/2}{n}(-R^2e^{i2\phi})^{-n}\,d\phi\tag2\\\\ &=\pi\tag3 \end{align}$$

where in going from $(2)$ to $(3)$ we exploited the uniform convergence of the series in $(2)$ to integrate term by term and used the fact that $\int_0^{2\pi}e^{im\phi}\,d\phi=2\pi \delta_{m0}$.

Putting together $(1)$ and $(2)$ we find that

$$\oint_{C_{DB}}\sqrt{1-z^2}\,dz=\pi\tag4$$

In addition, letting the radii, $\varepsilon$, of $\gamma_2$ and $\gamma_2$ approach $0$, we find that

$$\lim_{\varepsilon\to 0}\oint_{C_{DB}}\sqrt{1-z^2}\,dz=2\int_{-1}^1 \sqrt{1-x^2}\,dx\tag5$$

Finally, putting together $(1)$, $(3)$, and $(5)$ yields the coveted result

$$\int_{-1}^1\sqrt{1-x^2}\,dx=\frac\pi 2$$

as was to be shown using contour integration!

NOTE:

The methodology used herein is tantamount to using the "Residue at Infinity."

The residue at infinity is given by

$$\begin{align} \text{Res}\left(\sqrt{1-z^2}, z=\infty\right)&=i\text{Res}\left(\frac1{z^2}\sqrt{\frac1{z^2}-1}, z=0\right)\\\\ &=i\text{Res}\left(\frac1{z^3}\sqrt{1-z^2}, z=0\right)\\\\ &=-i/2 \end{align}$$

from which we find

$$\oint_{C_{DB}}\sqrt{1-z^2}\,dz=\pi$$

Mark Viola
  • 179,405
  • Very good, but is it possible to get $\oint_{|z|=R}\sqrt{1-z^2}dz=-\pi$ using the residue theorem somehow? – thedude Aug 06 '21 at 14:18
  • Also, which value of $n$ contributed to the integral from (2) to (3)? – thedude Aug 06 '21 at 14:19
  • @thedude Given the way the branch cuts are defined here (i.e., to ensure that $\int_{-1}^1 \sqrt{1-x^2},dx>0$), the integral $\oint_{|z|=R}\sqrt{1-z^2},dz=\pi$. For the second question, the Kronecker Delta , $\delta_{m0}$, is $0$ for all $m\ne 0$ and is equal to $1$ for $m=0$. So because of the extra $e^{i2\phi}$ in the integrand of $(2)$, only the term $n=1$ contributes. – Mark Viola Aug 06 '21 at 14:23
1

You can Cauchy's theorem to show that the integral over the dog bone contour is equal to the integral over the outer circle, and you can use the definition of the former integral to get that the integral over the dog bone contour is twice the integral in question. But this doesn't really help you evaluate the integral. The basic issue is that the functions in question don't have poles anywhere, so the residue theorem can't be used to give a numerical answer.

Zarrax
  • 44,950
  • Wait, I don't understand. First of all, I think the dog bone integral is $2$ times the integral in question, not $1-i$. Second, why can't the residue theorem be used? Can't I just say the residue is zero? (I mean, I know this would give the wrong answer, but what is the reason I can't say that, from first principles) – thedude Aug 06 '21 at 13:53
  • 1
    @thedude You have to use complex square roots, and you get a factor of $i$ or $-i$ when you wrap around a branch point. Depending on the branches used the result is a factor like $1 + i$ or $1 - i$. In addition, the residue theorem applies only when $f(z)$ is analytic on the domain inside the contour except at a finite set of poles. Here you are missing the segment $[-1,1]$ and the function you're integrating doesn't have poles in $[-1,1]$. – Zarrax Aug 06 '21 at 14:00
  • Please help me see how you can square what you are saying with Mark Viola's answer here: https://math.stackexchange.com/questions/1261515/dog-bone-contour-integral. They get a factor 2 and they use the residue theorem for the region outside of the contour, where the function is analytic (except for the residue at infinity). – thedude Aug 06 '21 at 14:07
  • 1
    He's using something called the "residue at infinity" where he switches from $f(z)$ to a function $-{1 \over z^2} f(1/z)$. That's a separate thing you can do, where you can use the residue theorem on $-{1 \over z^2} f(1/z)$ at $z = 0$. But it's not the residue theorem as you are trying to use it. – Zarrax Aug 06 '21 at 14:13
  • By the way, you're right in that it is twice the integral and not $1 + i$ times the integral, but the rest of what I said is true. – Zarrax Aug 06 '21 at 14:57