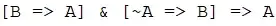Question on "Proof by contradiction"

Question

I am a little confused whether the following set of arguments can constitute a proof by contradiction:

Required to prove: Statement A is true.

Assumption: Suppose statement A is false.

We then show that if A is false then a (different) statement B is true.

But, statement B is true implies A is true.

Hence, A must be true.

These set of arguments feel a bit bizzare to me and perhaps might be incorrect. I am unable find a mistake.

If $\mathbf A$ is false then $\mathbf A$ is true, that's a contradiction. Do you have an actual proof that you feel unsure? — peterwhy, Aug 06 '21 at 00:45
@peterwhy Yes, I did have an actual proof. The proof comes from algebraic geometry and is quite technical. I managed to reduce it to statements A and B as above and check the individual steps as written above. I had previously not seen this usage of proof by contradiction, so I wanted to be sure., if it is OK. — Chen, Aug 06 '21 at 00:55
Also take a look at Point 3 here and its footnote, which I wrote two days ago. — ryang, Aug 06 '21 at 02:10

score 4 · Accepted Answer · edited Aug 06 '21 at 02:09

4

You start your proof from "let A be false". Now, using "true tools" you prove a particular statement which implies that A has to be true. So to sum up you prove that A is false implies A is true. This is a contradiction. For example:

A: there isn't a smallest rational number greater than zero.

Assumption: there is a smallest rational number greater than zero.

So, call him $r$.

Now you can take $r/2$.

So B: given a rational number $r$ greater than zero, there exists another rational number $r/2$ that is greater than zero and smaller than $r$.

So A.

edited Aug 06 '21 at 02:09

William A. Noble

388

answered Aug 06 '21 at 00:56

LuckyS

772

1

Thanks. The example helps a lot. – Chen Aug 06 '21 at 01:00
"you prove that A is false implies A is true. This is a contradiction" No it isn't, it is a (supposedly) valid implication that one could deduce at this point, but in fact one doesn't. Instead, but proving, under the assumption that A is false, that A is true you have arrived at a point where, by using the assumption a (supposedly) second time, one can easily derive a contradiction (still under that assumption). Then one can proceed with the proof by contradiction. – Marc van Leeuwen Aug 06 '21 at 09:55

score 2 · Answer 2 · answered Aug 06 '21 at 01:36

This technique is actually quite common. The answer above from LuckyS is a nice one. Here's my favorite simple example.

We have three beans, each one either white or black.
We will prove that there must a pair of beans of the same color.
Suppose this is not so.
Then the first two beans are not a pair of the same color, so one is white and the other is black.
Then if the third bean is white, there is a pair of white beans, and if the third bean is black, there is a pair of black beans.

score 1 · Answer 3 · answered Aug 06 '21 at 02:23

Yes, this is a proof by contradiction, but written in a different way.

You have two statements: $B \implies A$ and $\neg A \implies B$, both of which are true.

If you have come across proofs by contrapositive before, you will know that $B \implies A$ and $\neg A \implies \neg B$ are equivalent. This means that what you really have are the two statements

$$\neg A \implies B \\ \neg A \implies \neg B$$

This is a contradiction, and this is how one typically learns proofs by contradiction. So what you have is essentially the same thing, but with the second statement $\neg A \implies \neg B$ written as the equivalent $B \implies A$.

@Chen To be extremely clear, the pair of highlighted statements aren't in themselves a contradiction, but they lead to the contradiction $(B$ and $\lnot B)$ — and only when $\lnot A$ is true (in this case, presumed to be true). If, instead, $A$ is true, the pair of highlighted statements don't lead to any contradiction. — ryang, Aug 06 '21 at 04:55

Dan Christensen · Answer 4 · 2021-08-07T15:01:31.943

(Posted after a previous answer was accepted.)

We have the tautology:

We can verify this using a truth table. Or we can can prove it using a simplified form of natural deduction as below. We take the negation of proposition $A$ on line 4 to mean that "$A$ is assumed to be false" (a premise). Lines 4-9 are a proof by contradiction that $A$ must be true given the premise on line 1. (Screenshot from my proof checker)

score 1 · Answer 5 · answered Aug 06 '21 at 09:48

The way proof by contradiction works is that by assuming A is false, we can find some logical reasoning that shows that some known false statement B is true. Sometimes the key to a proof is that the false statement B is "A ^ ¬A", but it doesn't need to be that: B could be "1 = 2" or any other false statement.

Then, having shown that assuming ¬A means that the false statement B actually is true, we state that this is absurd, and conclude that ¬A must actually be false. Since ¬A is false, A must be true.

Question on "Proof by contradiction"

5 Answers5