2

$\newcommand{\Q}{\mathbb{Q}}\newcommand{\N}{\mathbb{N}}\newcommand{\Z}{\mathbb{Z}}$Recall the definitions of the tensor product $\otimes_{\mathbb{N}}$ of commutative monoids (see also this note by Harold Simmons) and of the Grothendieck group $K_0$ of a commutative monoid (see also wikipedia). Given commutative monoids $A$ and $B$, we can apply the universal property of $K_0$ to the diagram

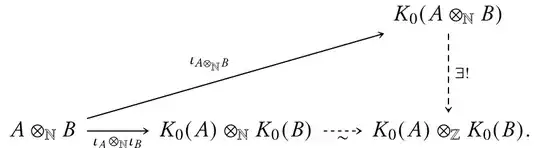
to get a morphism of abelian groups $$K^{\otimes}_{0|A,B}\colon K_{0}(A\otimes_{\mathbb{N}}B)\to K_{0}(A)\otimes_{\mathbb{Z}}K_{0}(B).$$ Since we also have an isomorphism $K^{\otimes,1}_{0}\colon K_{0}(\mathbb{N})\overset{\sim}{\dashrightarrow}\mathbb{Z}$, these morphisms endow $K_{0}$ with the structure of an oplax monoidal functor $$ (K_{0},K^{\otimes}_{0},K^{\otimes,1}_{0}) \colon (\mathsf{CMon},\otimes_{\mathbb{N}},\mathbb{N}) \longrightarrow (\mathsf{Ab},\otimes_{\mathbb{Z}},\mathbb{Z}). $$ (I think―I haven't actually checked the coherence conditions.)

Now, I'm quite confident that the map $K^\otimes_{0|A,B}$ is not always an isomorphism, so I'm trying to come up with a counterexample. Am I correct in thinking that $A=B=(\mathbb{Z},\cdot,1)$ is such an example?

On one side, we have $\mathbb{Z}\otimes_{\mathbb{N}}\mathbb{Z}\overset{\text{i think?}}{\cong}\Z\oplus\Z_{2}$, so \begin{align*} K_0(\Z\otimes_{\N}\Z) &\cong K_0(\Z\oplus\Z_2)\\ &\cong K_0(\Z)\oplus K_{0}(\Z_2)\\ &\cong \Q\oplus\Z_2, \end{align*} (where we've used the strong monoidality of $K_0$ with respect to direct sum), while on the other we have \begin{align*} K_0(\Z)\otimes_{\Z}K_0(\Z) &\cong \Q\otimes_{\Z}\Q\\ &\cong \Q \end{align*} (via here). Thus $$K_0(\Z\otimes_{\N}\Z)\cong\Q\oplus\Z_2\neq\Q\cong K_0(\Z)\otimes_{\Z}K_0(\Z).$$

Question

Are the above calculations correct? Moreover, what are some other examples (assuming this is indeed one >_<) of commutative monoids $A$ and $B$ such that the map $K_{0}(A\otimes_{\mathbb{N}}B)\to K_{0}(A)\otimes_{\mathbb{Z}}K_{0}(B)$ is not an isomorphism?

Emily
  • 1,114
  • (Note that this question is quite similar to mine, but different) – Emily Aug 04 '21 at 00:51
  • I don't know where you're getting $\mathbb{Z}\otimes_\mathbb{N}\mathbb{Z}\cong\mathbb{Z}\oplus\mathbb{Z}_2$ from. In any case, all the Grothendieck groups in your example are going to be trivial since you are inverting every element, including $0$, and inverting $0$ kills everything. – Eric Wofsey Aug 04 '21 at 01:17

1 Answers1

1

In fact, the canonical map $K_{0}(A\otimes_{\mathbb{N}}B)\to K_{0}(A)\otimes_{\mathbb{Z}}K_{0}(B)$ is always an isomorphism. One way to see this is by observing that if $M$ is a commutative monoid then $K_0(M)$ is naturally isomorphic to $\mathbb{Z}\otimes_{\mathbb{N}} M$ (where here $\mathbb{Z}$ is the additive monoid). You can prove this, for instance, by verifying that bilinear maps $\mu:\mathbb{Z}\times M\to N$ are in natural bijection with homomorphisms $f:M\to N$ that send each element of $M$ to an invertible element (by defining $\mu(a,m)=af(m)$ in one direction and defining $f(m)=\mu(1,m)$ in the other direction).

So, $$K_0(A\otimes_\mathbb{N} B)\cong \mathbb{Z}\otimes_\mathbb{N} A\otimes_{\mathbb{N}} B\cong (\mathbb{Z}\otimes_\mathbb{N}\mathbb{Z})\otimes_\mathbb{N} A\otimes_{\mathbb{N}} B\cong (\mathbb{Z}\otimes_\mathbb{N} A)\otimes_\mathbb{N}(\mathbb{Z}\otimes_\mathbb{N} B)\cong K_0(A)\otimes_\mathbb{N} K_0(B).$$ Since $\otimes_\mathbb{N}$ is the same as $\otimes_\mathbb{Z}$ when applied to commutative monoids that are actually already groups, this gives an isomorphism $K_{0}(A\otimes_{\mathbb{N}}B)\to K_{0}(A)\otimes_{\mathbb{Z}}K_{0}(B)$. It is then a matter of definition-chasing to confirm that this isomorphism is the same as the map you are considering (for instance, by verifying that they both send elements of the form $[a\otimes b]$ (which generate the group $K_{0}(A\otimes_{\mathbb{N}}B)$) to $[a]\otimes [b]$)).

There are several errors in your proposed example. I'm not sure how you got that $\mathbb{Z}\otimes_\mathbb{N}\mathbb{Z}\cong\mathbb{Z}\oplus\mathbb{Z}_2$; this does not seem correct since (for instance) the elements $p\otimes -1$ should be distinct invertible elements of $\mathbb{Z}\otimes_\mathbb{N}\mathbb{Z}$ for each prime $p$ whereas $\mathbb{Z}\oplus\mathbb{Z}_2$ has only finitely many invertible elements (assuming you mean the $\mathbb{Z}$ there to still be the multiplicative monoid). Also, $K_0(\mathbb{Z})=0$, not $\mathbb{Q}$, since adjoining an inverse to $0$ kills everything ($0\cdot x=0$ implies $x=1$ if $0$ becomes invertible).

Eric Wofsey
  • 330,363
  • Oh, this is excellent! Thank you! Would it be okay to ask a few more questions? 1) Why does $p$ need to be prime for $p\otimes_{\mathbb{N}}-1$ to be invertible in $\mathbb{Z}\otimes_{\mathbb{N}}\mathbb{Z}$? 2) On $K_0$'s and inverses of $0$, do we still have $K_0(\mathbb{Z}\setminus{0})\cong\mathbb{Q}^\times$? 3) Lastly, how does one describe $\mathbb{Z}\otimes_{\mathbb{N}}\mathbb{Z}$ explicitly (with $\mathbb{Z}$ again the multiplicative monoid)? (I think I'm still a bit confused about how to think about tensor products of commutative monoids :/) – Emily Aug 04 '21 at 03:06
  • 1
  • Eh, $p$ probably doesn't need to be prime. I was just thinking about primes specifically since they're the free generators of $\mathbb{Z}\setminus{0}$. 2) Yes, that's correct.
    • – Eric Wofsey Aug 04 '21 at 03:50
  • 1
  • I don't know the exact description. If you removed $0$ from both copies of $\mathbb{Z}$ then they would each be isomorphic to a direct sum of countably many copies of $\mathbb{N}$ and one copy of $\mathbb{Z}2$. When you tensor these together you get countably many copies of each of $\mathbb{N}$ and $\mathbb{Z}_2$ since tensor products distribute over direct sums. But then to actually get $\mathbb{Z}\otimes\mathbb{N}\mathbb{Z}$, you have to add back in all the elements and relations you get by including $0$. I don't know a clean description of the result of that.
    • – Eric Wofsey Aug 04 '21 at 03:52
  • 1
    I believe that the natural map $(\mathbb{Z}\setminus{0})\otimes(\mathbb{Z}\setminus{0})\to\mathbb{Z}\otimes\mathbb{Z}$ should be injective, so adding in $0$ doesn't give any new relations among the elements you already had. But I haven't worked out a complete proof of that. – Eric Wofsey Aug 04 '21 at 03:54
  • 1
    I think of tensor products of commutative monoids very similarly to how I think of tensor products of abelian groups (or of modules over a ring). My core intution for how to think about $A\otimes B$ (if $A$ and $B$ are abelian groups, say) is that you describe how to "build" $A$ out of $\mathbb{Z}$ (more formally, by "building" I mean taking colimits), and then do the same thing but starting with $B$ instead of $\mathbb{Z}$. One way to make this precise is the Eilenberg-Watts theorem, which says $-\otimes B$ is the unique colimit-preserving functor $Ab\to Ab$ that sends $\mathbb{Z}$ to $B$. – Eric Wofsey Aug 04 '21 at 03:59
  • 1
    For commutative monoids, you do the same thing, except the role of $\mathbb{Z}$ is played by $\mathbb{N}$ instead. So for instance, what is $\mathbb{Z}\otimes M$ (where here $\mathbb{Z}$ is additive)? Well, $\mathbb{Z}$ is obtained from $\mathbb{N}$ by adjoining an inverse to its generator, so $\mathbb{Z}\otimes M$ should be obtained by adjoining inverses to the generators of $M$, which just gives the Grothendieck group. – Eric Wofsey Aug 04 '21 at 04:01
  • Thank you so much! Your way of thinking about tensor products of commutative monoids/abelian groups is really nice! I'll go learn about the Eilenberg–Watts theorem to try to understand your point of view better :) – Emily Aug 04 '21 at 23:01
  • (By the way, I've opened another question about explicitly describing $\mathbb{Z}\otimes_{\mathbb{N}}\mathbb{Z}$ here, pointing to this discussion. This sounds like something with a very good chance of having been worked out before, so I think there's some value in asking it as a separate question―maybe someone already knows the answer. Also, I really like the description of $(\mathbb{Z}\setminus{0})\otimes_{\mathbb{N}}(\mathbb{Z}\setminus{0})$ you mentioned. Again, thank you so much!) – Emily Aug 04 '21 at 23:02