Is it just a coincidence that the solution to $y=x$, $y=mx+b$ ($m<1$) is the sum of an infinite geometric series with first term $b$ and ratio $m$?

Question

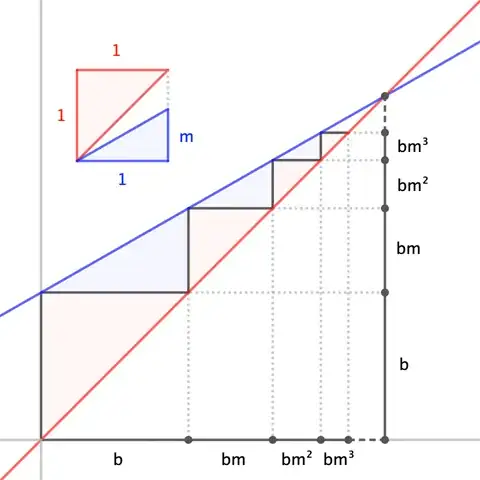
The solution for the system of linear equations of $y = x$ and $y = mx + b$ is $$x=y= \frac{b}{1-m}.$$ I noticed that this is also the sum of an infinite geometric series, where the first term is $b$ and common ratio is $m$ (granted $m$ is less than $1$):
$$ \frac{b}{1-m} = b + bm + bm^2 + \cdots bm^n + \cdots$$

Is this all a big coincidence or is there some deeper meaning to this relationship?

Answer 1

Note that, simultaneously considering the two equations $y=x$ and $y=mx+b$, we have,

$$\begin{align}y&=b+mx\\&=b+my\\&=b+m(b+mx)\\&=b+mb+m^2x\\&=b+mb+m^2y\\&=b+mb+m^2(mx+b)=\ldots\end{align}$$

Answer 2

Consider the following:

The reader is invited to investigate how to adjust the diagram when the line $y=x$ is replaced with $y=nx$, and then $y=nx+c$.

Answer 3

It follows by induction.

As $x = mx+b$ we can replace $x$ with $mx+b$ indefinitely.

$y = x \\= mx + b=m(mx+b) + b \\= m^2x + mb + b\\=m^2(mx+b)+mb+b \\= m^3x + m^2b + m b + b\\\dots\\b + mb + m^2b + m^3b + m^4b + ......$

This shouldn't be a surprise. If $|m| < 1$ then $b + mb + m^2b + m^3b + m^4b + ...... \\= b(1 + m + m^2 + m^2 + m^4 + ....)\\=b\frac 1{1-m}=\frac b{1-m}$

And if $x = mx + b$ we must have $x-mx = b$ so $x(1-m)=b$ so $x = \frac b{1-m}$.