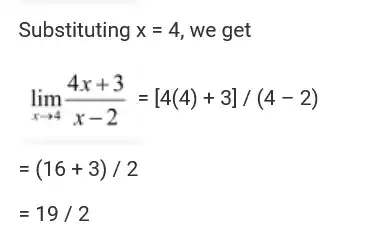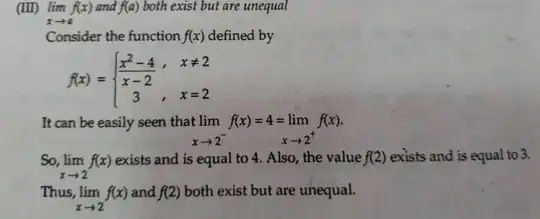5

As a high school student,I understand the basic,theoretical difference between the two, as in, limit is what that function approaches as the input approaches something (but never equal to it) or how it behaves near that point etc etc. But sometimes it doesn't seem to make sense. Like Some textbooks, when evaluating certain simple limits like this: enter image description here

They just substitute the value 4 and evaluate it like this:

enter image description here

But then how is it different than evaluating the function itself at that point? One can say that here the limit as well as the value at that point will be same, but I'm pointing out the method used here, SIMPLE SUBSTITUTION!

Along with a better understanding of difference between the two, I would also like to understand what it means when both the value at that point and limit are defined but still they are different.Because I have been told that limits are used to evaluate undefined values/expressions like $\frac{0}{0}$ , $\infty / \infty$, $0^{0}$ etc. For Ex-

enter image description here

Both are well defined, still different.What does that difference mean in cases like these?

Kashi
  • 95
  • If $f(x)$ is defined in a neighborhood of $(x_0)$, $f(x)$ is defined at $x_0$, and $f(x)$ is a continuous function at $x_0$, then $\lim_{x \to x_0} f(x) = f(x_0).$ Here, a neighborhood of radius $\delta > 0$, around $x_0$ denotes all $x$ such that $0 < |x - x_0| < \delta.$ The function $$f(x) = \frac{4x+3}{x-2}$$ is well defined at $x = 4$, defined in a neighborhood around $x = 4$, and continuous at $x=4$. – user2661923 Aug 02 '21 at 05:09
  • Re previous comment, it could be argued that it involves circular reasoning re I am assuming (re continuity) what it is being asked to prove. There are other results in Real Analysis that establish that $f(x)$ is a continuous function at $x = 4$. For example, both the numerator and denominator are continuous functions at $x = 4$, and the quotient of two continuous functions is itself a continuous function, as long as the denominator at the pertinent point is not equal to $0$. – user2661923 Aug 02 '21 at 05:15
  • You may have a look at this answer: https://math.stackexchange.com/a/1822706/72031 – Paramanand Singh Aug 03 '21 at 15:47
  • Also you should remember that limits are not evaluated by SIMPLE SUBSTITUTION, but by using theorems meant to evaluate limits. Have you seen theorems which deal with limit of sum, difference, product, quotient of two functions? You need to use such theorems combined with another two simple results: $\lim_{x\to a} x=a, \lim_{x\to a} k=k$. For a first course in calculus, it is not necessary to know proofs of such theorems, but one must learn how to use them. – Paramanand Singh Aug 03 '21 at 15:52
  • I hope your teacher or textbook does mention these theorems which are very important to have a solid grasp on limits. – Paramanand Singh Aug 03 '21 at 15:56
  • @ParamanandSingh , I think they do (textbook does, teacher not so much) and yes proofs of all aren't there. I will definitely read your answer. Thank you! – Kashi Aug 03 '21 at 16:56

2 Answers2

5

The definition of the limit of $f(x)$ at $x=x_0$ looks at the behavior of $f$ as you approach $x_0$, but does not actually look at the value at $x_0$.

So for example, if you have the function $$f(x) = \begin{cases}0, &x\neq 0\\1, &x=0\end{cases}$$ then $f(0)=1$ but $\lim_{x\to 0} f(x) = 0.$

For continuous functions, $f(x_0) = \lim_{x\to x_0} f(x)$. (That the limits of a function exist, and are equal to simply evaluating the function, is after all the definition of continuity.) Many textbooks will evaluate limits by plugging in $x_0$ when the function in question is "obviously" continuous at $x_0$. Most functions you encounter "in the wild" are continuous almost everywhere, including polynomials, rational functions, trig functions, and compositions made of these pieces. To be fully rigorous, you ought to prove that a particular function is continuous before plugging in to evaluate a limit, but in practice as you become more experienced and comfortable you will start to skip this step.

The reason the indeterminate forms like $\frac{0}{0}$ are emphasized so much is that they're one of the most common cases where a function's continuity is not obvious, and where a careful analysis using the limit definitions is sometimes necessary.

user7530
  • 49,280
2

The trick your textbook is using the is the result:

A real valued function $f:D \rightarrow \mathbb{R}$ on domain $D \subseteq \mathbb{R}$ is continuous at $c \in \mathbb{R}$ if $\lim_{x \rightarrow c} f(x) = f(c)$.

So the textbook is basically saying "we know this function $ f(x) = \frac{4x+3}{x-2} $ is continuous at $x = 4$, so we can simply take $\lim_{x \rightarrow 4} f(x) = f(4). $"

But wait a minute! How do we know the function $ f(x) = \frac{4x+3}{x-2} $ is continuous at $x = 4$??? In order to show that $ f(x) = \frac{4x+3}{x-2} $ is continuous at $x = 4$ don't we need to first show that $\lim_{x \rightarrow 4} f(x) = f(4) $????

So the textbook is more or less using some circular logic to tackle this problem. But for many practical purposes, we know from prior experience where common functions are continuous/discontinouous. If we know that the function is continuous at the point of the limit, we can use simple substitution.

A more rigorous proof that $\lim_{x \rightarrow 4} \frac{4x+3}{x-2} = \frac{19}{2}$ would go like this:

Let $\epsilon > 0$. Choose $\delta = \min\{\frac{2}{11}\epsilon , 1\}$ and let $\vert x - 4 \vert < \delta$.

Then, $\vert f(x) - \frac{19}{2}\vert = \vert\frac{4x+3}{x-2} - \frac{19}{2}\vert = \vert \frac{-11x+44}{2x-4} \vert = 11 \vert x-4 \vert \vert \frac{1}{2x-4} \vert$.

Note that $ \frac{1}{6} \le \vert \frac{1}{2x-4} \vert \le \frac{1}{2}$, so,

$ 11 \vert x-4 \vert \vert \frac{1}{2x-4} \vert \le \frac{11}{2} \vert x-4 \vert < \frac{11}{2}\delta \le \epsilon $. Therefore, $\lim_{x \rightarrow 4} \frac{4x+3}{x-2} = \frac{19}{2}$. $\square$

You'd learn this is a college intro to real analysis course, but for a HS intro to calculus course it's a bit overkill. They want you to get a conceptual of limits before going into rigour (that is if you ever do). For many applied STEM professions, the basic concepts of limits are more than enough.

Brian Lai
  • 770