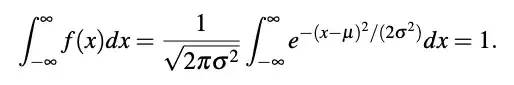Checking that the Normal Distribution is a valid probability density function

Question

I am trying to check that this integral evaluates to 1, but so far I haven't had much success doing so. I tried expanding out the exponent so that I'd have

$$\frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^{\infty} e^{-\frac{x^2 - 2\mu x + \mu^2}{2 \sigma ^2}} \,dx$$

This can be re-written as

$$\frac{1}{\sqrt{2\pi\sigma^2}} (\int_{-\infty}^{\infty} e^{-\frac{x^2}{2 \sigma ^2}} \,dx \cdot \int_{-\infty}^{\infty} e^{\frac{2 \mu x}{2 \sigma ^2}} \,dx \cdot \int_{-\infty}^{\infty} e^{-\frac{\mu ^2}{2 \sigma ^2}} \,dx)$$

The first integral gives $\frac{\sqrt{\pi}}{1/\sqrt{2 \sigma^2}}$, which does cancel out with the coefficient, but I'm not sure how to evaluate the other two integrals. Ideally those two would multiply to be 1, but their integration seems divergent to me.

Could someone help me see what I did wrong or if there are other ways to get the desired output?

Answer 1

Don't expand the exponent. Rather observe that (assuming convergence of the improper integrals) $$\int_{-\infty}^\infty f(x)\,\mathrm dx = \int_{-\infty}^\infty f(x+c)\,\mathrm dx$$

Answer 2

Recall that Gaussian Integral is equal to the square root of pi: $$\int_{-\infty}^\infty e^{-x^2}\,\mathrm dx = \sqrt{\pi}$$ We can somehow leverage this fact but we cannot directly apply to x at this point. Instead, denote new variable y as the following: $$ y = \frac{x-\mu}{\sqrt{2\sigma^2}} $$ If you take derivates in both sides, you'll get: $$ dy = \frac{1}{\sqrt{2\sigma^2}}*dx$$ Now, replace y and dy in the original Gaussian formula and substitute the value of Gaussian integral (square root of pi) at last:

$$\frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^\infty -e^{\frac{(x-\mu)^2}{{2\sigma^2}}}\,\mathrm dx = \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty e^{-y^2} \sqrt{2\sigma^2} \mathrm dy = \frac{1}{\sqrt{2\pi\sigma^2}} \sqrt{2\sigma^2} \sqrt \pi = 1 $$