I was inspired to return to an old problem I came up with after seeing
This was the problem of finding the analogs of other trigonometric functions which would parametrize a certain graph $f(x,y)=1$ or $y=f(x)$ taking the polar curve angle $\theta=\theta_0$ and finding the length of the curve for one intersection of $f(x,y)+0$. These are also called the abcissa and ordinate of the intersection.
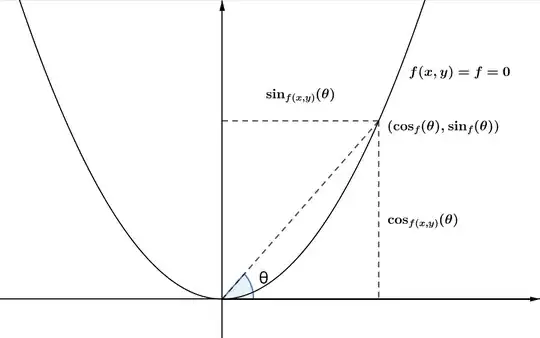
This just boils down to finding trigonometric functions which parametrize the curve f(x,y). This is easy, but the goal is have the distance from the intersection of the angle with the curve to the x,y-axis be the these functions $(x(\theta), y(\theta))$. Here is how to find such functions. For convention, let $x(\theta)=\cos_{f(x,y)=0}(\theta)=\cos_f(x),y(\theta)=\sin_{f(x,y)=0}(\theta)=\sin_f(x)$. Sorry for the notation, but it is intuitive. Here is how to find such functions easily:
$$f(x,y)=0,y=x\tan(\theta)\implies f(x,x\,\tan(\theta))=0\implies x=\cos_{f(x,y)=0}(\theta),y=\sin_{f(x,y)=0}(\theta)$$
There is not an easy inverse function for both arguments. However, when y is given explicitly you can solve for the alternate trigonometric functions which sometimes works through recursion.
$$\frac{f(x)}{x}=\tan(\theta)\implies x=f^{-1}(x\,tan(\theta))= f^{-1}(f^{-1}(f^{-1}(…x…\,\tan(\theta))\,\tan(\theta))\,\tan(\theta))=\cos_f(\theta)\implies y=\sin_f(\theta)=\tan(\theta) f^{-1}(f^{-1}(f^{-1}(…x…\tan(\theta))\tan(\theta))\tan(\theta))$$
Unless you use an inversion theorem, then you cannot always solve for the inverse of y=f(x), unless if there is a closed form inverse. For example if you modeled the trigonometric equations with y=x tan(θ) and f(x)=\cos(x), you would find that $x(\theta)=\cos_{\cos(x)(θ)}=\cos_f(x), y(\theta)=x(\theta)\tan(\theta)$ would be the parametrization for $\cos(x)$ for $(x(\theta),y(\theta))$. This uses the cardinal sine/ sinc function. Note $x_0$ here is just a parameter as a consequence of the nesting:
$$\frac{\sin(x)}{x}=\text{sinc}(x)=\tan(\theta)\implies \cos_f(x)=\sin^{-1}(\sin^{-1}(…x_0 \tan(\theta))\tan(\theta)…),\frac{\cos(x)}x=\tan(\theta)\implies \cos_f(x)=\cos^{-1}(\cos^{-1}(…x_0\tan(\theta))\tan(\theta)…)$$
Here are the results in this graph. Notice that lengths of the legs of the right triangle, like in the diagram, will give the derived modified cosine and sine functions. These new trigonometric functions are now based on sine and cosine graph instead of the circle.
Of course we can just use an inversion theorem, in the link above, to find the alternate trigonometric functions. Here is a formula that will not need to be used very much as we can usually find these alternate trigonometric functions. This is the general result for a function with explicit $y=f(x)$ with the Lagrange Inversion Theorem. This uses the Bell polynomials and the rising factorial
$$\frac {f(x)}x=\tan(\theta)\implies x(\theta)=\cos_f(x)\left(\text{Inverse of }\frac yx\right)[\tan(\theta)]=a+\sum_{n=1}^\infty\lim_{x\to a}\frac{d^{n-1}}{dx^{n-1}}\left[\left(\frac{x-a}{\frac{f(x)}{x}-\frac{f(a)}{a}}\right)^n\right]\frac{\left(\tan(\theta)-\frac{f(a)}{a}\right)^n}{n!}=\sum_{k=0}^\infty c^{-n}_1\sum_{K=1}^{k-1}(-1)^K k^{(K)}B_{k-1,K}\left(\frac{c_2}{2c_1}, \frac{c_3}{3c_1},…, \frac{c_{n-k+1}}{(n-k+1)c_1}\right),\frac{f(x)}x=\sum_{n=0}^\infty c_n\frac{x^n}{n!},n\ge 2$$
All I did was use linked Lagrange Inversion theorem formulas.
As a side note, I will leave you with the alternate trigonometric functions for $a|x|^n+b|x|^n=1$. Here is an interactive graph The analogue for these trigonometric functions is just $$\mathrm{x(\theta)=\pm\frac{1}{\sqrt[n]{a+b|tan(\theta)|^n}},y(\theta)= \pm\frac{tan(\theta)}{\sqrt[n]{a+b|tan(\theta)|^n}}}$$
Here is another special case if one takes $f(x)=ax^2+bxy+cy^2+dx+ey+f=0$ in this fixed graph. Notice how the formula for a=c=1,b=d=e=0,f=-1 is a special case with the unit circle with the usual x=cos(θ),y=sin(θ). These types of analogues for the trigonometric functions are:
$$x(\theta)=-\frac{\sqrt{{(e\tan(\theta)+d))^2-4f・(c\tan^2(\theta)+b\tan(\theta)+a)}}+e\tan(\theta)+d}{2(c\tan^2(\theta)+b\tan(\theta)+a)},y(\theta)=x(\theta)tan(\theta)$$
The secant and cosecant analogues are just $\frac{1}{x(\theta)}$ and $\frac{1}{y(\theta)}$. The tangent and cotangent analogues are almost always $\tan(θ)$ and $\cot(θ) $because $\mathrm{y(\theta)=x(\theta)tan(\theta)}$.
These graphs now have the analogue (co)secant graphs. Please see the graphs for examples of trigonometric function analogues. The question now is how to solve $$y=x\tan(\theta),f(x,y)=0\implies f(x,x\tan(\theta))=0$$ for $x$ in exact form, not necessarily closed form, using any method except approximation. Please correct me and give me feedback!