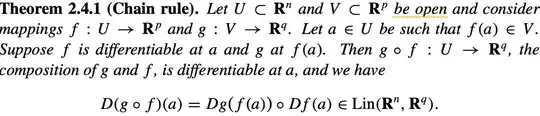- Yes, your proof is right (I just checked my copy of Duistermaat and Kolk and indeed you didn't invoke anything not already proven).
- Sure, one can introduce the vector $h$ to see that the evaluation of both sides is the same. But to me this seems 'obvious'. Indeed I could reverse the question and ask you why in step 1 you did not verify explicitly (by plugging in an arbitrary $x$) that $g\circ f = \lambda f_1+f_2$ (I'm guessing you didn't do this because it seemed obvious enough because the functions $f$ and $g$ were literally constructed to make this equation true).
- I'm not sure if this proof can be simplified, but the authors probably said it is obvious because all you're doing is applying the chain rule to carefully chosen functions.
So, if it was me, I would have just written the following for a proof:
(Define $f,g$ as you have done). Then, $\lambda f_1+f_2=g\circ f$, so
\begin{align}
D(\lambda f_1+f_2)_a&=D(g\circ f)_a\\
&=Dg_{f(a)}\circ Df_a\tag{chain rule}\\
&=g\circ Df_a\tag{$g$ is linear}\\
&=g\circ ((Df_1)_a,(Df_2)_a)\\
&=\lambda (Df_1)_a+(Df_2)_a
\end{align}
So, the only theorems being invoked are the chain rule and that linear maps have derivatives equal to themselves.
Of course, having now proven this theorem as a consequence of the chain rule, you should also prove it directly from the definition: i.e prove (using triangle inequality) that
\begin{align}
\frac{\bigg\|\,\,\,(\lambda f_1+f_2)(a+h) - (\lambda f_1+f_2)(a) - [\lambda (Df_1)_a(h)+(Df_2)_a(h)]\,\,\,\,\bigg\|}{\|h\|}\to 0
\end{align}
as $h\to 0$.
By the way, one can prove things in a different order. Usually, one proves linearity of the derivative directly, and then proves the chain rule. From here, all other facts can be derived, for example, the fact that if $f_1,f_2$ are differentiable at $a$ and $f(x):=(f_1(x)f_2(x))$ then $f$ is also differentiable at $a$ and $Df_a(h)=((Df_1)_a(h),(Df_2)_a(h))$ can be proven as follows:
define $\iota_1:\Bbb{R}^{p_1}\to\Bbb{R}^{p_1}\times\Bbb{R}^{p_2}$ and $\iota_2:\Bbb{R}^{p_2}\to\Bbb{R}^{p_1}\times\Bbb{R}^{p_2}$ by $\iota_1(x)=(x,0)$ and $\iota_2(y)=(0,y)$. Then given two mappings $f_1:\Bbb{R}^n\to\Bbb{R}^{p_1}$ and $f_2:\Bbb{R}^{n}\to\Bbb{R}^{p_2}$, we define $f:\Bbb{R}^n\to\Bbb{R}^{p_1}\times\Bbb{R}^{p_2}$ as $f(x)=(f_1(x),f_2(x))$.
Then, it is easily verified that $f=\iota_1\circ f_1+\iota_2\circ f_2$, and that $\iota$'s are linear transformations. So,
\begin{align}
Df_a(h)&=D(\iota_1\circ f_1+\iota_2\circ f_2)_a(h)\\
&=[\iota_1\circ (Df_1)_a](h)+[\iota_2\circ (Df_2)_a](h)\\
&=\bigg((Df_1)_a(h),(Df_2)_a(h)\bigg)
\end{align}
(of course in the second equal sign, I did many steps at once; I used additivity of derivatives, used the chain rule, and that $\iota_1,\iota_2$ are linear so they are their own derivatives).
The idea of introducing such "auxillary" mappings $\iota$ is very common when you're trying to prove more complicated maps are differentiable (for example one can formulate a very general product rule)