What is a covector?

Question

I have been watching a youtube series about tensors for beginners and there he described covectors as essentially functions which take in vectors as input and return a scalar output. And he also told us how to visualise them in 2d. But however I had to find out whats the usuage of covectors, so I googled it and I found this answer What is a covector and what is it used for? But this is way above my level since I yet dont know a lot of what he is talking about like tangent spaces and actually any kind of spaces or fields. Like what does it even mean for a finite vector space to be over a field?? So whats the best place for me to start learning so that I can understand this answer?

Answer 1

a covector, say $\omega$ for example, isn't just a function $\omega:V \to \mathbb{R}$ that takes a vector and gives a real number. it has to be linear. as for $u,v\in V$ and $a,b \in \mathbb{R}$: $$\omega(av+bu)=a\omega(v)+b\omega(u)$$ this property has nice consequences. you probably know that in a vector space, for example the vector space of directed line segments on the $\mathbb{R}^2$ plane, you can choose a set of linearly independent vectors and and express any other vector as a linear combination of them. for example $v$ here can be written as a linear combination of $\{e_1,e_2\}$. 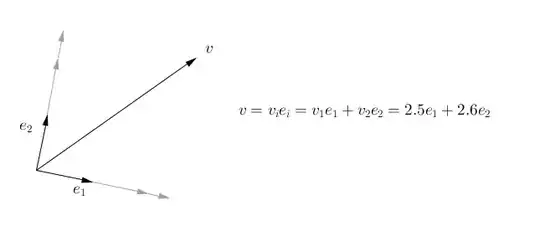so if we applied our function $\omega$ on $v$ using the linearity property : $$\omega(v)=\omega(v_ie_i)=\omega(v_1e_1+v_2e_2)=v_1\omega(e_1)+v_2\omega(e_2)$$ let $\omega_i=\omega(e_i)$ be the value of $\omega$ applied on our chosen basis $\{e_1,e_2\}$. so: $$\omega(v)=\omega_1v_1+\omega_2v_2$$ so if you want to express any vector as linear combination of these two basis vectors. the value of $\omega$ applied at this vector can be easily calculated if you know its value at the chosen basis. Now, why are these kind of functions called covectors? well consider these two linear functions $\{\theta_1,\theta_2\}$: $$\theta_1(e_1)=1 \; ; \; \theta_2(e_1)=0 \; ; \; \theta_2(e_1)=0 \; ; \; \theta_2(e_2)=1$$

applying $\theta_i$ to a vector $v$ gives us the $i$-th component of it: $$\theta_1(v)=v_1\theta_1(e_1)+v_2\theta_1(e_2)=v_1 \\ \theta_2(v)=v_1\theta_2(e_1)+v_2\theta_2(e_2)=v_2$$

so:

$$\omega(v)=v_1\omega_1+v_2\omega_2=\omega_1 \theta_1(v)+\omega_2 \theta_2(v) = (\omega_1 \theta_1+\omega_2 \theta_2)(v)$$

so the linear function $\omega$ can be expressed as a linear combination of $\{\theta_1,\theta_2\}$. so this set of linear functions can be added, scalar-multiplied and be written as a linear combination of two "basis" linear functions. so they form a vector space called the dual space to $V$ and has the symbol $V^*$.

but what if we choose other basis instead of $\{e_1,e_2\}$? how will the components of $v$ change? how will the dual vector basis $\{\theta_1,\theta_2\}$ change? this is the topic of the youtube series you are following now which I assume is eigenchris's series and I think he does a beautiful job explaining this.

in this answer I assumed that you know at least "classical" vectors, directed line segments, and how to add and scale them and what is a linear combination. hope this was helpful.

Answer 2

I'm not going to answer what is a vector/covector/tangent space/vector space over a field etc, because these are simply too many topics to cover for a single MSE answer.

It seems like you're lacking a firm foundation in linear algebra, because all your questions all the subject of a first course in proof-based linear algebra. Specifically, all the basics you need are covered in chapters 1 and 2 of Friedberg Insel Spence's linear algebra book (I'm sure other books are available, but this is the one I studied from). Chapter 1 is about vector spaces over a field, and chapter 2 is about linear transformations. Section 2.6 talks about dual spaces. Elements of the dual space $V^*$ of a vector space $V$ are often called covectors.

This may seem like a huge detour learning about tensors, and ok maybe it is. But I can guarantee you that you'll learn the material much better by having a firm foundation, and learn linear algebra "the proper way" (if not it's like trying to ride a motorcycle without even learning to ride a tricycle).

Once you have the basic understanding of linear algebra, and multivariable calculus in $\Bbb{R}^n$, we can then come to differential geometry, which is where we encounter vector fields, covector fields, and more generally tensor fields, which are mappings which assign to each point $p$ of the manifold a certain tensor $\xi(p)$ defined on the tangent space $T_pM$. Once again, you shouldn't even try to tackle this beast without having studied the basic linear algebra.