What kinds of PDE can't be solved by separation of variables? Except those without boundary and which are non-linear? Does it matters with the shape of solution domain?
When should I use addition or division (not multiplication) to separate variables?
Thanks a lot!
Here just to expand my comments into an answer.
What kind of equations can't be solve using separation of variables except non-linear and inhomogeneous ones?
Short answer: For equations that have constant coefficient, live in a nice domain, with some appropriate boundary condition, we can solve it by separation of variables. If we change one of above three conditions, then most of the time we can't solve it by separation of variables.
An example: a heuristic is that those equations which describe a physical phenomena involving non-constant convection can't be solved by separation of variables. The famous one is the linear transport equation $$ \frac{\partial u}{\partial t} + \vec{a}(t,x)\cdot \nabla u = 0,\tag{1} $$ it describes a quantity $u$ "flows" within the vector field $\vec{a}(t,x)$, given boundary condition we can solve it, but not by separation of variable. Using 1D setting and constant $a$: $$ u_t + au_x = 0,\quad u(x,0) = g(x) $$ This equation looks simple enough to be solved by separation of variables. From method of characteristics, the solution is $u = g(x-at)$ which is a constant for any permissible initial condition $g$. The solution "propagates" along with time and is constant on its characteristics $x-at = 0$. If using separation of variables, the solution we get will be in the form (try it your self): $$ u(x,t) =\sum B_i e^{C_i(x-at)}, $$ this tell us that $u(x,0)$ must be a linear combination of $B e^{Cx}$. However, if we choose some initial condition $g$ that can not be decomposed into plane wave superposition form, then this equation can't be separable. For example on $[0,aT]\times [0,T]$, if $g(x) = \ln x$, $u$ is: $$ u(x,t) = \ln (x-at). $$ EDIT: I just realized above can be solved by separation, for $\ln x$ on a finite interval can be written in Fourier expansion. If we change the initial condition to $g(x) = 1/x^2$ on $[0,\pi]$, of which doesn't have a Fourier series expansion on interval containing $0$, then this equation can't solved by separation of variables.
Does it matters with the shape of solution domain? YES! It matters a lot, normally separability relies on if we can express the domain as a "rectangle", i.e., $[a_1, b_1] \times [a_2,b_2]\times\cdots\times [a_n,b_n]$, not matter in cylinderical type of coordinates or polar coordinates. For example, MATLAB's famous icon:
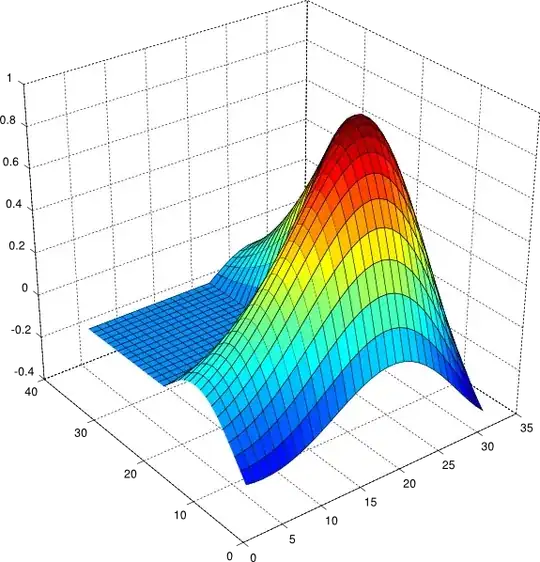
is the eigenfunction for Dirichlet-Neumann mixed boundary problem for
$$
-\Delta u =\lambda u
$$
in the L-shape domain. This can't be solved using separation of variable in contrast of that the intuition for above problem is that it can be solved using separation variables. Well, let's analyze it a bit. Homogeneous Dirichlet boundary condition is imposed in the L-shaped non-convex corner, while other sides just have homogeneous Neumann boundary condtion. Every eigenfunction $u_n$'s behavior near the non-convex corner is
$$
u_n \sim \alpha_n r^{2/3}\sin \Big(\frac{2}{3}\theta\Big) + o(r^{2/3}) \approx \alpha_n(x^2+y^2)^{1/3}\sin\left(\frac{2}{3}\arctan (y/x)\right),
$$
(in the second quadrant we need add another $\pi$ to the $\arctan$). While on the outer rim (side adjacent to convex corners) it behaves like
$$u_n\sim \beta_n(a\cosh(n\pi x) + b\sinh(n\pi x))\cos(n\pi y),
$$
or the $\cos$ is in $x$ and hyperbolic functions are in $y$. To describe both singular and wave like behavior on both sides of L-shaped domain, $u_n = X(x)Y(y)$ this kind of a one shot expression does not exist.
A remark: If we added diffusion in (1): $$ \frac{\partial u}{\partial t} = \nabla \cdot\Big(a(t,x)\nabla u + \vec{b}(t,x) u\Big).\tag{2} $$ This can't be solved using separation either.
However, if we don't have the convective type of terms $\vec{b}(t,x)\cdot \nabla u$ (this term is $\nabla \cdot (\vec{b} u)$ when $\vec{u}$ is divergence free), and diffusion constant only depends on space, then we can separate the time variable from the solution in (2), even for general domain. In general where $L$ is elliptic and does not depend on time, consider $$ \frac{\partial u}{\partial t} = Lu, \quad u(x,0) = g(x).\tag{3} $$ If we can find orthonormal eigenfunctions $\{w_n\}$ for the eigenvalue problem in space (for general domain we can't separate variables) $$ L w = \lambda w, $$ then for (3) the solution can be written as: $$ u(x,t) =\sum^{\infty}_{n=1} e^{-\lambda_n t} \langle g(x), w_n(x) \rangle w_n(x), $$ which has the form of time variable being separated.
Also Willie Wong gave a more specific answer for hyperbolic equation here: when does a separate-variable series solution exist for a PDE
